内蒙古自治区呼伦贝尔市阿荣旗2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 下列函数中,不是一次函数的是( )A、 B、 C、 D、3. 在▱ABCD中,若∠B=70°,则∠D=( )A、35° B、70° C、110° D、130°4. 若代数式有意义,则实数x的取值范围是( )A、 B、且 C、 D、且5. 下列各组数中不能作为直角三角形的三边长的是( ).A、1.5,2,2 B、7,24,25 C、6,8,10 D、9,12,156. 下列计算正确的是( )A、 B、 C、 D、7. 如图,正方形中, , 则 ( )
 A、 B、 C、 D、8. 点和都在直线上,则与的大小关系是( )A、 B、 C、 D、无法确定9. 已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
A、 B、 C、 D、8. 点和都在直线上,则与的大小关系是( )A、 B、 C、 D、无法确定9. 已知,如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )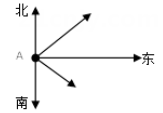 A、25海里 B、30海里 C、35海里 D、40海里10. 如图,在长方形 中无重叠放入面积分别为 和 的两张正方形纸片,则图中空白部分的面积为( )
A、25海里 B、30海里 C、35海里 D、40海里10. 如图,在长方形 中无重叠放入面积分别为 和 的两张正方形纸片,则图中空白部分的面积为( )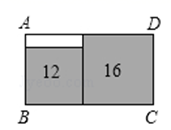 A、 B、 C、 D、11. 如图,矩形 中, , ,点 从点 出发,沿 向终点 匀速运动,设点 走过的路程为 , 的面积为 ,能符合题意反映 与 之间函数关系的图象是( )
A、 B、 C、 D、11. 如图,矩形 中, , ,点 从点 出发,沿 向终点 匀速运动,设点 走过的路程为 , 的面积为 ,能符合题意反映 与 之间函数关系的图象是( )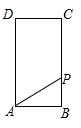 A、
A、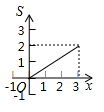 B、
B、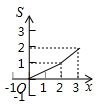 C、
C、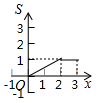 D、
D、 12.
12.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
 A、2 B、2.2 C、2.4 D、2.5
A、2 B、2.2 C、2.4 D、2.5二、填空题
-
13. 已知函数与函数的图象交于点 , 则不等式的解集是 .
 14. 如图所示,在数轴上点A所表示的数为a,则a的值为 .
14. 如图所示,在数轴上点A所表示的数为a,则a的值为 .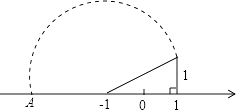 15. 如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是 .
15. 如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是 . 16. 甲、乙两人5次射击命中的环数如下:
16. 甲、乙两人5次射击命中的环数如下:甲:7,9,8,6,10
乙:7,8,9 ,8, 8
则这两人5次射击命中的环数的平均数 = =8,方差 .(填“>”、“<”或“=”)
17. 如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,正方形A , B , C的面积分别是8cm2 , 10cm2 , 14cm2 , 则正方形D的面积是cm2 .
三、解答题
-
18. 计算19. 计算: .20. 已知等腰三角形周长为20.(1)、写出底边长y关于腰长x的函数解析式(x为自变量);(2)、写出自变量取值范围;(3)、在直角坐标系中,画出函数图象.21. 如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
 22. 某商场统计了每个营业员在某月的销售额,绘制了如下统计图.
22. 某商场统计了每个营业员在某月的销售额,绘制了如下统计图.
解答下列问题:
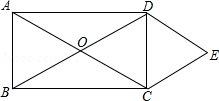
(1)、设营业员的月销售额为x(单位:万元).商场规定:当时为不称职,当时为基本称职,当时为称职,当时为优秀.试求出不称职、基本称职、称职、优秀四个层次营业员人数所占百分比,并画出相应的扇形图.(2)、根据(1)中规定,所有称职和优秀的营业员月销售额的中位数、众数和平均数分别是多少?(3)、为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡达到或超过这个标准的营业员将受到奖励.如果要使得称职和优秀的所有营业员的半数左右能获奖,奖励标准应定为多少元?并简述其理由.23. 如图,矩形ABCD的对角线相交于点O,DE//AC,CE//BD,求证:四边形OCED是菱形.
 24. 阅读下面问题:
24. 阅读下面问题:==-1;
1/+=1×(-)/ (+)/ (-)=-;
1/+=1×(-)/ (+)/ (-)=-;
试求:
(1)、=;(2)、当n为正整数时,=;(3)、求+++…++的值.25. 某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳上网费的方式有:方式一:每月80元包月;方式二:每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示;方式三:以0小时为起点,每小时收费1.6元,月收费不超过120元.若设一用户每月上网x小时,月上网费为y元.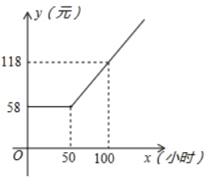 (1)、根据图象,写出方式二中y(元)与x(小时)的函数关系式;(2)、试写出方式三中y(元)与x(小时)的函数关系式;(3)、若此用户每月上网60小时,选用哪种方式上网其费用最少?最少费用是多少?
(1)、根据图象,写出方式二中y(元)与x(小时)的函数关系式;(2)、试写出方式三中y(元)与x(小时)的函数关系式;(3)、若此用户每月上网60小时,选用哪种方式上网其费用最少?最少费用是多少?