内蒙古自治区巴彦淖尔市临河区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 函数y= + 中自变量x的取值范围是( )A、 B、 且 C、 且 D、2. 下列运算正确的是( )A、 =±6 B、4 ﹣3 =1 C、 =6 D、 =63. 一组数据的方差可以用式子 表示,则式子中的数字50所表示的意义是( )A、这组数据的个数 B、这组数据的平均数 C、这组数据的众数 D、这组数据的中位数4. 如图,四边形ABCD是边长为10的正方形,点E在正方形内,且 , 又 , 则阴影部分的面积是( )
 A、76 B、24 C、48 D、885. 下列命题是真命题的是( )A、有一个角是直角的四边形是矩形 B、对角线互相平分且相等的四边形是矩形 C、一组对边平行且相等的四边形是矩形 D、对角线互相垂直平分的四边形是矩形6. 如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=6,BD=8,点E是AD边的中点,连接OE,则OE的长为( )
A、76 B、24 C、48 D、885. 下列命题是真命题的是( )A、有一个角是直角的四边形是矩形 B、对角线互相平分且相等的四边形是矩形 C、一组对边平行且相等的四边形是矩形 D、对角线互相垂直平分的四边形是矩形6. 如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=6,BD=8,点E是AD边的中点,连接OE,则OE的长为( ) A、10 B、 C、5 D、47. 已知函数 , 则下列直线是该直线的函数的图象的是( )A、
A、10 B、 C、5 D、47. 已知函数 , 则下列直线是该直线的函数的图象的是( )A、 B、
B、 C、
C、 D、
D、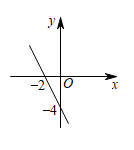 8. 若顺次连接四边形ABCD各边的中点所得到的四边形是矩形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形9. 均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为( )
8. 若顺次连接四边形ABCD各边的中点所得到的四边形是矩形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形9. 均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
10. 如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )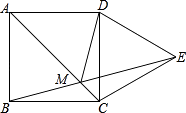 A、75° B、60° C、54° D、67.5°
A、75° B、60° C、54° D、67.5°二、填空题
-
11. 一组数据2022,2022,2022,2022,2022的方差是 .12. 若一组数据2,3,x,5,7的众数为7,则这组数据的中位数为 。13. 如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别是线段AO,BO的中点.若 , , 则的周长是cm.
 14. 如图,直线与交点的横坐标为 . 则关于的不等式的解集为 .
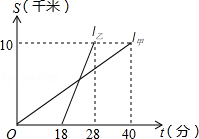
14. 如图,直线与交点的横坐标为 . 则关于的不等式的解集为 .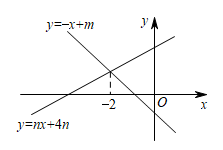 15. 已知两条线段的长分别为 cm、 cm,那么能与它们组成直角三角形的第三条线段的长是 .16. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
15. 已知两条线段的长分别为 cm、 cm,那么能与它们组成直角三角形的第三条线段的长是 .16. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8km后遇到甲;④乙出发6分钟后追上甲.其中正确的有(填所有正确的序号).
三、解答题
-
17.(1)、计算:;(2)、计算:18. 某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别
A
B
C
D
处理方式
迅速离开
马上救助
视情况而定
只看热闹
人数
m
30
n
5

请根据表图所提供的信息回答下列问题:
(1)、统计表中的 m= , n=;(2)、补全频数分布直方图;(3)、若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?19. 如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.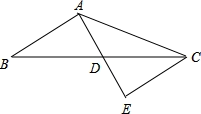 (1)、求证:△AEC是直角三角形.(2)、求BC边的长.20. 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示.
(1)、求证:△AEC是直角三角形.(2)、求BC边的长.20. 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示. (1)、第20天的总用水量为多少米3?(2)、当x≥20时,求y与x之间的函数关系式;(3)、种植时间为多少天时,总用水量达到7000米3?21. 如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD、EC.
(1)、第20天的总用水量为多少米3?(2)、当x≥20时,求y与x之间的函数关系式;(3)、种植时间为多少天时,总用水量达到7000米3?21. 如图,在△ABC中,AB=AC,点D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD、EC. (1)、求证:△ADC≌△ECD;(2)、若BD=CD,求证:四边形ADCE是矩形.22. 如图,直线的解析表达式为 , 且 与x轴交于点D,直线经过点A,点B,直线 ,交于点C.
(1)、求证:△ADC≌△ECD;(2)、若BD=CD,求证:四边形ADCE是矩形.22. 如图,直线的解析表达式为 , 且 与x轴交于点D,直线经过点A,点B,直线 ,交于点C. (1)、求直线的解析表达式;(2)、求的面积;(3)、在直线上存在异于点C的另一点P,使得的面积等于面积,请直接写出点P的坐标.23. 某商店购进甲、乙两种商品,甲商品每件进价20元,售价25元.乙商品每件进价30元,售价40元.(1)、若甲、乙两种商品共购进100件,设购进甲商品x件,销售完此两种商品的总利润为y元,求出y与x的函数关系式.(2)、该商家计划最多投入2800元用于购进此两种商品共100件,则至少要购进多少件甲种商品.(3)、若售完这些商品,商家可获得最大利润是多少元?24. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)、求直线的解析表达式;(2)、求的面积;(3)、在直线上存在异于点C的另一点P,使得的面积等于面积,请直接写出点P的坐标.23. 某商店购进甲、乙两种商品,甲商品每件进价20元,售价25元.乙商品每件进价30元,售价40元.(1)、若甲、乙两种商品共购进100件,设购进甲商品x件,销售完此两种商品的总利润为y元,求出y与x的函数关系式.(2)、该商家计划最多投入2800元用于购进此两种商品共100件,则至少要购进多少件甲种商品.(3)、若售完这些商品,商家可获得最大利润是多少元?24. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE. (1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
(1)、求证:CE=AD;(2)、当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)