辽宁省营口市鲅鱼圈区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 函数的自变量x的取值范围是( )A、 B、 C、 D、x≥0且x≠12. 下列计算正确的是( )A、 B、 C、 D、3. 下列条件中,不能判断一个三角形是直角三角形的是( )A、三条边的比为2∶3∶4 B、三条边满足关系a2=b2﹣c2 C、三条边的比为1∶1∶ D、三个角满足关系∠B+∠C=∠A4. 下列表格反映了某公司员工的工资情况,该公司的应聘者最应该关注的数据是( )
职位
普工
文员
经理
董事长
人数
8
6
2
1
工资/元
2200
2600
4000
12000
A、平均数 B、众数与中位数 C、方差 D、最大数据5. 如图是小军设计的一面彩旗,其中 , ,点 在 上, ,则 的长为( ) A、 B、 C、 D、6. 生物活动小组的同学们观察某植物生长,得到该植物高度 (单位: )与观察时间 (单位:天)的关系,并画出如图所示的图象( 轴),该植物最高的高度是( )
A、 B、 C、 D、6. 生物活动小组的同学们观察某植物生长,得到该植物高度 (单位: )与观察时间 (单位:天)的关系,并画出如图所示的图象( 轴),该植物最高的高度是( ) A、 B、 C、 D、7. 如图所示,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
A、 B、 C、 D、7. 如图所示,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( ) A、△AOB的面积等于△AOD的面积 B、当AC⊥BD时,它是菱形 C、当OA=OB时,它是矩形 D、△AOB的周长等于△AOD的周长8. 如图,在平面直角坐标系中,点M是直线y=﹣x上的点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为( )
A、△AOB的面积等于△AOD的面积 B、当AC⊥BD时,它是菱形 C、当OA=OB时,它是矩形 D、△AOB的周长等于△AOD的周长8. 如图,在平面直角坐标系中,点M是直线y=﹣x上的点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为( )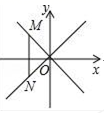 A、0≤m≤4 B、﹣4≤m≤0 C、m≥﹣4 D、﹣4≤m≤49. 如图,在矩形ABCD中, , ,点M,N同时从点A出发,分别沿 及 方向匀速运动,速度均为每秒1个单位长度,当一个点到达终点时另一个点也停止运动,连接MN,设运动时间为t秒,MN的长为d,则下列图象能大致反映d与t的函数关系的是( )
A、0≤m≤4 B、﹣4≤m≤0 C、m≥﹣4 D、﹣4≤m≤49. 如图,在矩形ABCD中, , ,点M,N同时从点A出发,分别沿 及 方向匀速运动,速度均为每秒1个单位长度,当一个点到达终点时另一个点也停止运动,连接MN,设运动时间为t秒,MN的长为d,则下列图象能大致反映d与t的函数关系的是( )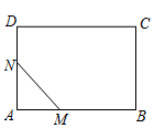 A、
A、 B、
B、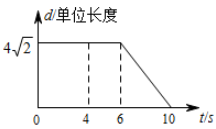 C、
C、 D、
D、 10. 如图,正方形ABCD的边长为2,点E为AD的中点,连接BE,将 沿BE折叠,点A的对应点为F.连接CF,则CF的长为( )
10. 如图,正方形ABCD的边长为2,点E为AD的中点,连接BE,将 沿BE折叠,点A的对应点为F.连接CF,则CF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中, , , , , 垂足为D,则AD的长为 .
 12. 如图,在菱形ABCD中,点E为AB上一点,DE=AD , 连接EC . 若∠ADE=36°,则∠BCE的度数为 .
12. 如图,在菱形ABCD中,点E为AB上一点,DE=AD , 连接EC . 若∠ADE=36°,则∠BCE的度数为 .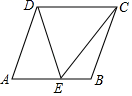 13. 在本学期的五次数学检测中,甲同学的成绩如下:92,89,88,87,94,乙同学的成绩如下:78,88,98,94,98,两名同学成绩比较稳定的是 (“甲”或“乙”).14. 在一次函数的图象上有一点 , 已知点到轴的距离为 , 则点的坐标为 .15. 如图,在四边形 ABCD 中,AD∥BC,DE⊥BC,垂足为点 E,连接 AC 交DE 于点 F,点 G 为 AF 的中点,∠ACD=2∠ACB,若 DC=5,则 AF 的长为 .
13. 在本学期的五次数学检测中,甲同学的成绩如下:92,89,88,87,94,乙同学的成绩如下:78,88,98,94,98,两名同学成绩比较稳定的是 (“甲”或“乙”).14. 在一次函数的图象上有一点 , 已知点到轴的距离为 , 则点的坐标为 .15. 如图,在四边形 ABCD 中,AD∥BC,DE⊥BC,垂足为点 E,连接 AC 交DE 于点 F,点 G 为 AF 的中点,∠ACD=2∠ACB,若 DC=5,则 AF 的长为 . 16. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .
16. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .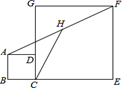
三、解答题
-
17. 计算:(1)、2;(2)、(3﹣2+ )÷2 .18. 如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了 m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C.
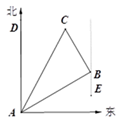 (1)、求A、C两点之间的距离;(2)、确定目的地C在营地A的北偏东多少度方向.19. 已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.
(1)、求A、C两点之间的距离;(2)、确定目的地C在营地A的北偏东多少度方向.19. 已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.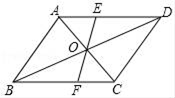 20. 如图,在四边形ABCD中, ,点E为AB的中点, ,交AB于点E, ,求CE的长.
20. 如图,在四边形ABCD中, ,点E为AB的中点, ,交AB于点E, ,求CE的长.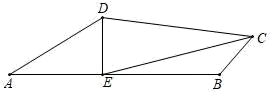 21. 某校举行八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图、趣题巧解、数学应用、魔方复原,每个项目得分按一定百分比折算后记入总分.下表为甲、乙、丙三位同学得分情况(单位:分)
21. 某校举行八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图、趣题巧解、数学应用、魔方复原,每个项目得分按一定百分比折算后记入总分.下表为甲、乙、丙三位同学得分情况(单位:分)七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68
(1)、比赛后,甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四个项目得分分别按10%,40%,20%,30%折算记入总分,根据猜测,求出甲的总分;(2)、本次大赛组委会最后决定,总分为80分以上(包括80分)的学生获一等奖,现获悉乙、丙的总分分别是70分、80分,甲的七巧板拼图、魔方复原两项得分折算后分数和是20分,问甲能否获得这次比赛的一等奖.22. 如图,在平面直角坐标系中,一次函数y=kx十b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.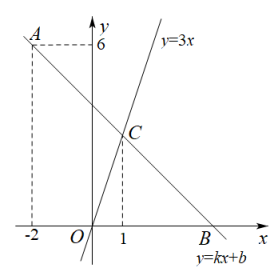 (1)、求k,b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集;(3)、若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.23. 如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题,并说明理由.
(1)、求k,b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集;(3)、若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.23. 如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,请回答下列问题,并说明理由. (1)、四边形ADEF是什么四边形;(2)、当△ABC满足什么条件时,四边形ADEF是矩形;(3)、当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在.24. 为更新树木品种,某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵,其中甲种树苗的单价为6元/棵,购买乙种树苗所需费用y(元)与购买数量x(棵)之间的函数关系如图所示.
(1)、四边形ADEF是什么四边形;(2)、当△ABC满足什么条件时,四边形ADEF是矩形;(3)、当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在.24. 为更新树木品种,某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵,其中甲种树苗的单价为6元/棵,购买乙种树苗所需费用y(元)与购买数量x(棵)之间的函数关系如图所示.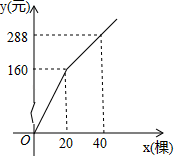 (1)、求出y与x的函数关系式;(2)、若在购买计划中,乙种树苗的数量不超过35棵,但不少于甲种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.25. 将一矩形纸片OABC放在平面直角坐标系中,O为原点,点C在x轴上,点A在y轴上,OA=9,OC=15.
(1)、求出y与x的函数关系式;(2)、若在购买计划中,乙种树苗的数量不超过35棵,但不少于甲种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.25. 将一矩形纸片OABC放在平面直角坐标系中,O为原点,点C在x轴上,点A在y轴上,OA=9,OC=15. (1)、如图1,在OA上取一点E,将△EOC沿EC折叠,使点O落在边AB上的点D处,求直线EC的解析式;(2)、如图2,在OA,OC边上选取适当的点M,N,将△MON沿MN折叠,使O点落在AB边上的点D'处,过点D'作D'G⊥CO,垂足为G,交MN于点T,连接OT,判断四边形OTD'M的形状,并说明理由;(3)、在(2)的条件下,若点T的坐标为(6,),点P在直线MN上,坐标轴上是否存在点Q,使以M,D',Q,P为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
(1)、如图1,在OA上取一点E,将△EOC沿EC折叠,使点O落在边AB上的点D处,求直线EC的解析式;(2)、如图2,在OA,OC边上选取适当的点M,N,将△MON沿MN折叠,使O点落在AB边上的点D'处,过点D'作D'G⊥CO,垂足为G,交MN于点T,连接OT,判断四边形OTD'M的形状,并说明理由;(3)、在(2)的条件下,若点T的坐标为(6,),点P在直线MN上,坐标轴上是否存在点Q,使以M,D',Q,P为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.