辽宁省沈阳市沈北新区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 下列各式从左边到右边的变形,是因式分解的为( )A、 B、 C、 D、2. 如图,用不等式表示数轴上所示的解集,正确的是( )
 A、或 B、或 C、 D、3. 下列命题是假命题的是( )A、平行四边形是中心对称图形 B、多边形的外角和都等于 C、五边形的内角和是 D、三角形的一个外角等于和它不相邻的两个内角的和4. 下列给出的条件中,能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠B=∠C;∠A=∠D C、AB=CD,CB=AD D、AB=AD,CD=BC5. 如图,点 、 、 、 、 都在方格子的格点上,若 是由 绕点 按顺时针方向旋转得到的,则旋转的角度为( )
A、或 B、或 C、 D、3. 下列命题是假命题的是( )A、平行四边形是中心对称图形 B、多边形的外角和都等于 C、五边形的内角和是 D、三角形的一个外角等于和它不相邻的两个内角的和4. 下列给出的条件中,能判断四边形ABCD是平行四边形的是( )A、AB∥CD,AD=BC B、∠B=∠C;∠A=∠D C、AB=CD,CB=AD D、AB=AD,CD=BC5. 如图,点 、 、 、 、 都在方格子的格点上,若 是由 绕点 按顺时针方向旋转得到的,则旋转的角度为( ) A、60° B、135° C、45° D、90°6. 1.已知点第二象限,则的取值范围是( )A、 B、 C、 D、7. 点 先向左平移3个单位长度,再向上平移2个单位长度得到的点的坐标是( )A、 B、 C、 D、8. 如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( )
A、60° B、135° C、45° D、90°6. 1.已知点第二象限,则的取值范围是( )A、 B、 C、 D、7. 点 先向左平移3个单位长度,再向上平移2个单位长度得到的点的坐标是( )A、 B、 C、 D、8. 如图,△ABC中,AB=AC,∠A=36°,BD是AC边上的高,则∠DBC的度数是( ) A、18° B、24° C、30° D、36°9. 如图,在中, , 将绕着点顺时针旋转后,得到 , 且点在上,则的度数为( )
A、18° B、24° C、30° D、36°9. 如图,在中, , 将绕着点顺时针旋转后,得到 , 且点在上,则的度数为( ) A、42° B、48° C、52° D、58°10. 平行四边形一边长 12cm,那么它的两条对角线的长度可能是( )A、8cm 和 16cm B、10cm 和 16cm C、8cm 和 14cm D、8cm 和 12cm
A、42° B、48° C、52° D、58°10. 平行四边形一边长 12cm,那么它的两条对角线的长度可能是( )A、8cm 和 16cm B、10cm 和 16cm C、8cm 和 14cm D、8cm 和 12cm二、填空题
-
11. 分式有意义的条件是: .12. 计算: .13. 如果关于x的不等式(a+1)x>a+1(a≠-1)可以变形为x<1,那么a的取值范围是 .14. 正多边形的一个外角等于20°,则这个正多边形的边数是 .15. 如图所示,△ABC中,AB=AC,过AC上一点E作DE⊥AC,EF⊥BC,垂足分别为E,F,若∠BDE=140°,则∠DEF= .
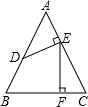 16. 在 中, , , ,点 在 边上,点 为 边上的动点,点 、 分别为 , 的中点,则 的最小值是.
16. 在 中, , , ,点 在 边上,点 为 边上的动点,点 、 分别为 , 的中点,则 的最小值是.
三、解答题
-
17. 解不等式及不等式组,并把解集在数轴上表示出来.
 (1)、;(2)、;(3)、 .18. 把下列各式因式分解.(1)、;(2)、;(3)、 .19. 计算(1)、;(2)、;(3)、;(4)、已知, , , 是的三边,求证: .20. 已知:如图,在▱中,、是对角线上的两点,且 , 求证: .
(1)、;(2)、;(3)、 .18. 把下列各式因式分解.(1)、;(2)、;(3)、 .19. 计算(1)、;(2)、;(3)、;(4)、已知, , , 是的三边,求证: .20. 已知:如图,在▱中,、是对角线上的两点,且 , 求证: . 21. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
21. 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.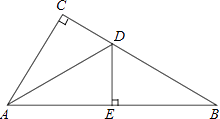 (1)、求证:△ACD≌△AED;(2)、若∠B=30°,CD=1,求BD的长.22. 供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?23. 某小区计划购买甲、乙两种树苗共棵进行绿化,已知甲种树苗每棵元,乙种树苗每棵元.(1)、若购买这批树苗共用了元,求甲、乙两种树苗各购买了多少棵?(2)、若购买这批树苗的钱不超过47000元,问应选购甲种树苗至少多少棵?24. 如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)、求证:△ACD≌△AED;(2)、若∠B=30°,CD=1,求BD的长.22. 供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?23. 某小区计划购买甲、乙两种树苗共棵进行绿化,已知甲种树苗每棵元,乙种树苗每棵元.(1)、若购买这批树苗共用了元,求甲、乙两种树苗各购买了多少棵?(2)、若购买这批树苗的钱不超过47000元,问应选购甲种树苗至少多少棵?24. 如图,直线y=kx+b经过点A(-5,0),B(-1,4)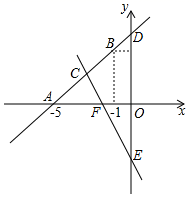 (1)、求直线AB的表达式;(2)、求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;(3)、根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.
(1)、求直线AB的表达式;(2)、求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;(3)、根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.