辽宁省沈阳市和平区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 许多数学符号蕴含着对称美,在下列数学符号中,既是轴对称图形,又是中心对称图形的符号是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式组 的解在数轴上表示为( )A、
2. 不等式组 的解在数轴上表示为( )A、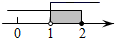 B、
B、 C、
C、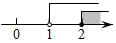 D、
D、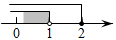 3. 下列因式分解正确的是( )A、 B、 C、 D、4. 下列各式从左到右的变形一定正确的是( )A、 B、 C、 D、5. 若顺次连结四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、平行四边形 C、对角线互相垂直的四边形 D、对角线相等的四边形6. 正多边形的每一个外角都等于45°,则这个多边形的边数是( )A、6 B、7 C、8 D、97. 如图,在平行四边形中 , 以点B为圆心,适当长度为半径作弧,分别交 , 于点M,N,再分别以M,N为圆心,以大于的长为半径作弧,两弧相交于点P,作射线交于点E,交的延长线于点F,则的长度为( )
3. 下列因式分解正确的是( )A、 B、 C、 D、4. 下列各式从左到右的变形一定正确的是( )A、 B、 C、 D、5. 若顺次连结四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、平行四边形 C、对角线互相垂直的四边形 D、对角线相等的四边形6. 正多边形的每一个外角都等于45°,则这个多边形的边数是( )A、6 B、7 C、8 D、97. 如图,在平行四边形中 , 以点B为圆心,适当长度为半径作弧,分别交 , 于点M,N,再分别以M,N为圆心,以大于的长为半径作弧,两弧相交于点P,作射线交于点E,交的延长线于点F,则的长度为( ) A、1 B、 C、2 D、38. 下列命题正确的是( )A、等腰三角形底边上的中线垂直于腰 B、等腰三角形的一边长为4,另一边长为9,则这个三角形的周长为17 C、若分式有意义,则 D、一组对边相等另一组对边平行的四边形是平行四边形9. 某市在创建全国文明城市的行动中,对一段4000米路段进行整修,为了减少施工对城市交通的影响,实际施工时每天的工效比计划增加 , 结果提前4天完成任务.设计划每天整修x米,根据题意所列方程正确的是( )A、 B、 C、 D、10. 如图,与都是等边三角形,连接 , 若将绕点C顺时针旋转,当点A、C、E在同一条直线上时,线段的长为( )
A、1 B、 C、2 D、38. 下列命题正确的是( )A、等腰三角形底边上的中线垂直于腰 B、等腰三角形的一边长为4,另一边长为9,则这个三角形的周长为17 C、若分式有意义,则 D、一组对边相等另一组对边平行的四边形是平行四边形9. 某市在创建全国文明城市的行动中,对一段4000米路段进行整修,为了减少施工对城市交通的影响,实际施工时每天的工效比计划增加 , 结果提前4天完成任务.设计划每天整修x米,根据题意所列方程正确的是( )A、 B、 C、 D、10. 如图,与都是等边三角形,连接 , 若将绕点C顺时针旋转,当点A、C、E在同一条直线上时,线段的长为( ) A、 B、 C、或 D、或
A、 B、 C、或 D、或二、填空题
-
11. 分解因式: .12. 若函数的图象如图所示,则不等式的解集是 .
 13. 化简的结果为 .14. 如图,点A为x轴负半轴上一点,过点A作轴,与直线交于点B,将沿直线平移个单位长度得到 , 若点A的坐标为 , 则点的坐标是 .
13. 化简的结果为 .14. 如图,点A为x轴负半轴上一点,过点A作轴,与直线交于点B,将沿直线平移个单位长度得到 , 若点A的坐标为 , 则点的坐标是 . 15. 如图,在四边形中中,点G是对角线的中点,点E、F分别是的中点, . 则的度数是 .
15. 如图,在四边形中中,点G是对角线的中点,点E、F分别是的中点, . 则的度数是 . 16. 在中, , 点D为的中点,点E在边上,将沿着翻折,使点C落在点F处,当时, .
16. 在中, , 点D为的中点,点E在边上,将沿着翻折,使点C落在点F处,当时, .
三、解答题
-
17. 因式分解:18. 解方程:19. 解不等式组: .20. 如图,在等边三角形中,点E是边上的一点,过点E作交于点D,作 , 交的延长线于点F.
 (1)、求证:;(2)、当时,请直接写出的面积.21. 在平面直角坐标系中,点A,B的坐标分别为将线段平移,点A,B的对应点分别为点C,D,且点C坐标为连接 .
(1)、求证:;(2)、当时,请直接写出的面积.21. 在平面直角坐标系中,点A,B的坐标分别为将线段平移,点A,B的对应点分别为点C,D,且点C坐标为连接 . (1)、直接画出四边形;(2)、四边形的面积为面积单位;(3)、点E是x轴上一动点,当时,请直接写出点E的坐标.22. 如图,点E,F是对角线上的两点,且 .
(1)、直接画出四边形;(2)、四边形的面积为面积单位;(3)、点E是x轴上一动点,当时,请直接写出点E的坐标.22. 如图,点E,F是对角线上的两点,且 . (1)、求证:四边形是平行四边形.(2)、若 .
(1)、求证:四边形是平行四边形.(2)、若 .①线段长为 .
②四边形的面积为 .
23. 暑假期间,某校部分家长组织学生到户外开展劳动实践活动,一名学生由一名家长陪同,家长联系了甲乙两家组织机构,他们的报价相同,每位学生的报价比家长少20元,按报价计算,家长的总费用为10000元,学生的总费用为9600元,(1)、求每位学生报价是多少元?(2)、经协商,甲机构的优惠条件是:家长全价,学生都按8折收费:乙机构的优惠条件是:家长、学生都按m(m为正整数)折收费,他们选择了总费用较少的乙机构,请直接写出m的最大值.24.(1)、如图1,在正方形中,点E,F分别在边 , 上,且 , 连接 , . 求证: , ; (2)、如图2,若将边长为4的正方形折叠,使得点A落在的中点E处,折痕为 , 点G在边上,点F在边上,则折痕;(3)、如图3,在正方形中, , , 则的最小值为 . (直接填空)25. 如图1,在平面直角坐标系中,直线交y轴于点 , 交x轴于点 , 以为直角边在第一象限内作等腰直角三角形 , .
(2)、如图2,若将边长为4的正方形折叠,使得点A落在的中点E处,折痕为 , 点G在边上,点F在边上,则折痕;(3)、如图3,在正方形中, , , 则的最小值为 . (直接填空)25. 如图1,在平面直角坐标系中,直线交y轴于点 , 交x轴于点 , 以为直角边在第一象限内作等腰直角三角形 , .

 (1)、求直线的函数表达式:(2)、如图2,点D的坐标为 , 连接 , 将绕点B逆时针旋转得 , 连接交x轴于点F,请直接写出的长;(3)、如图3,射线与y轴交于点G,在第四象限内有一点H,当的面积为3,且的面积为9时连接 , 将线段 , 从点B出发,沿射线的方向平移,平移后的线段记为(点在射线上),点M为y轴上的动点,当是以为直角边的等腰直角三角形时,请直接写出点M的坐标.
(1)、求直线的函数表达式:(2)、如图2,点D的坐标为 , 连接 , 将绕点B逆时针旋转得 , 连接交x轴于点F,请直接写出的长;(3)、如图3,射线与y轴交于点G,在第四象限内有一点H,当的面积为3,且的面积为9时连接 , 将线段 , 从点B出发,沿射线的方向平移,平移后的线段记为(点在射线上),点M为y轴上的动点,当是以为直角边的等腰直角三角形时,请直接写出点M的坐标.