辽宁省沈阳市法库县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列等式中，从左到右的变形是因式分解的是（）

A、 $x (x - 2) = x^{2} - 2 x$ B、 $x + 2 = x (1 + \frac{2}{x})$ C、 $x^{2} - 4 = (x + 2) (x - 2)$ D、 ${(x + 1)}^{2} = x^{2} + 2 x + 1$

查看试题解析
3. 以下列线段a，b，c的长为三边的三角形中，不能构成直角三角形的是（）

A、 $a = 7 ， b = 24 ， c = 25$ B、 $a = b = 5 ， c = 5 \sqrt{2}$ C、 $a ： b ： c = 3 ： 4 ： 5$ D、 $a = 13 ， b = 14 ， c = 15$

查看试题解析
4. 在平面直角坐标系中，若将三角形上各点的横坐标都加上 $5$ ，纵坐标保持不变，则所得图形在原图形的基础上（）

A、向左平移了 $5$ 个单位长度 B、向下平移了 $5$ 个单位长度 C、向上平移了 $5$ 个单位长度 D、向右平移了 $5$ 个单位长度

查看试题解析
5. 多边形的内角和不可能为（）

A、180° B、540° C、1080° D、1200°

查看试题解析
6. 已知 $▱$ ABCD中，∠A+∠C=200°，则∠B的度数是（）

A、100° B、160° C、80° D、60°

查看试题解析
7. 已知不等式组 ${\begin{array}{l} x - 2 ＜ 0 \\ x + 1 \geq 0 \end{array}$ ，其解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
8. 下列分式计算错误的是（）

A、 $\frac{x}{y} = \frac{x \cdot a}{y \cdot a} (a \neq 0)$ B、 $\frac{- x + y}{x} = - \frac{x - y}{x}$ C、 $\frac{9 - x^{2}}{x^{2} - 3 x} = \frac{3 + x}{x}$ D、 $\frac{a}{x - y} + \frac{a}{y - x} = 0$

查看试题解析
9. 如图，在△ABC中，∠A=90°，∠C=30°，BC的垂直平分线交AC于点D，交BC于点E，若ED=3，则AC的长为（）

A、 $3 \sqrt{3}$ B、9 C、12 D、6

查看试题解析
10. 如图，直线 $y = x + 2$ 与直线 $y = a x + c$ 相交于点 $P (m ， 3)$ ，则关于x的不等式 $x + 2 \leq a x + c$ 的解为（）

A、 $x \leq 1$ B、 $x < 1$ C、 $x \leq 3$ D、 $x \geq 1$

查看试题解析

二、填空题

11. 分解因式 $2 x^{2} - 8 x + 8 =$ ．

查看试题解析
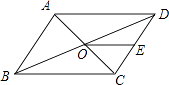
12. 若分式 $\frac{x^{2} - 1}{x + 1}$ 有意义，则x满足的条件是．

查看试题解析
13. 如果等腰三角形的一个角为50°，那么它的顶角为．

查看试题解析
14. 如图，▱ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为．

查看试题解析
15. 如图， $△ A B C$ 中， $A C = B C = 13$ ，把 $△ A B C$ 放在平面直角坐标系中，且点A，B的坐标分别为 $(2 ， 0)$ ， $(12 ， 0)$ ，将 $△ A B C$ 沿x轴向左平移，当点C落在直线 $y = - x + 8$ 上时， $△ A B C$ 平移的距离为．

查看试题解析
16. 如图，平面直角坐标系中，点A（0，3）和B（4，0），点M（8，m）为坐标平面内一动点，且ΔABM为等腰三角形，则点M的坐标为．

查看试题解析

三、解答题

17. 解方程： $\frac{3 - x}{x - 4} = 1 - \frac{1}{4 - x}$ ．

查看试题解析
18. 解不等式组 ${\begin{array}{l} x + 1 \geq 0 ① \\ \frac{x + 1}{2} - 1 \leq \frac{x}{3} ② \end{array}$ ，并写出所有整数解．

查看试题解析
19. 先化简，再求值： $\frac{m^{2} - 4 m + 4}{m - 1} \div (\frac{3}{m - 1} - m - 1)$ ，其中 $m = \sqrt{2} - 2$ .

查看试题解析
20. 如图，已知 $A (- 2 ， 3) ， B (- 3 ， 1) ， C (- 1 ， 2)$ ．

(1)、 $△ A B C$ 绕O逆时针旋转 $90 °$ ，得到 $△ A_{1} B_{1} C_{1}$ ，画出旋转后的 $△ A_{1} B_{1} C_{1}$ ；并直接写出点 $B_{1}$ 的坐标；

(2)、作出 $△ A B C$ 关于原点O的中心对称图形 $△ A_{2} B_{2} C_{2}$ ．并直接写出点 $B_{2}$ 的坐标．

查看试题解析
21. 如图，在 $▱ A B C D$ 中， $∠ A B C = 45 °$ ，过点A作 $A E ⊥ C D$ 于点E，连接BE，延长EA至点F，使 $A F = C E$ ，连接DF．求证： $D F = B E$ ．

查看试题解析
22. 如图，点B、C、D在一直线上，△ABC和△ADE都是等边三角形，

(1)、请找出图中的全等三角形，并说明理由；

(2)、求证：EB∥AC．

查看试题解析
23. 为加快产品生产的效率，某工厂将使用A，B两种型号机器生产产品，已知A型机器比B型机器每小时多生产10kg，且A型机器生产600kg所用时间与B型机器生产500kg所用时间相等．

(1)、求这两种机器每小时分别生产多少kg产品？

(2)、该工厂为了在每小时以内至少完成1000kg产品生产的任务量，决定使用A，B两种型号机器共18台，并且同时开始生产产品，那么至少需要A型号机器多少台？

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A C B = 90 ° ， C D ⊥ A B$ 于点D，BO平分 $∠ D B C$ ，交CO于点O， $O E ∥ A C$ ，交AB于点E，连接CE．

(1)、求证： $△ B O E ≌ △ B O C$ ；

(2)、求证：CE平分 $∠ A C D$ ；

(3)、若 $B C = 10 ， B D = 6$ ，请直接写出OB的长度．

查看试题解析
25. 如图，直线 $y = - x + 4$ 分别交x轴、y轴于A，B两点，直线BC与x轴交于点 $C (- 2 ， 0)$ ， P是线段AB上的一个动点（点P与A，B不重合）．

(1)、求直线BC的函数表达式；

(2)、设动点P的横坐标为t， $△ P O A$ 的面积为S．
①求出S与t的函数关系式；
②在线段BC上存在点Q，使得四边形COPQ是平行四边形，请直接写出点Q的坐标．

查看试题解析