辽宁省葫芦岛市连山区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 下列x的值能使二次根式 有意义的是( )A、-2 B、-1 C、0 D、12. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 在平面直角坐标系中有一个点A(﹣4,3),则点A到坐标原点O的距离是( )A、﹣5 B、5 C、 D、4. 满足下列条件的△ABC不是直角三角形的是( )A、∠A:∠B:∠C=3:4:5 B、BC=1,AC=2,AB= C、BC:AC:AB=3:4:5 D、BC=1,AC=2,AB=5. “按情就是命令,防控就是责任!”在去年新冠肺炎疫情爆发期间,我区教师发扬不畏艰险、无私奉献的精神,挺身而出,协助社区做好疫情监测、排查、防控等工作.现将50名教师参加社区工作时间 (单位:天)的情况统计如下:
时间 (天)
15
25
35
45
教师人数
4
6
7
13
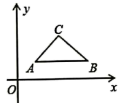
20
下面是对这50名教师参加社区工作时间的推断:
①平均数一定在40~50之间;②平均数可能在40~50之间;③中位数一定是45;④众数一定是50.其中正确的推断是( )
A、①④ B、②③ C、③④ D、②③④6. 已知数据1,2,3,3,4,5,则下列关于这组数据的说法错误的是( )A、众数是3 B、平均数是3 C、方差是2 D、中位数是37. 正比例函数y=kx的图象经过一、三象限,则一次函数y=﹣kx+k的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 已知直线l:y=2x+4,把直线l向右平移6个单位得到直线l1 , 则直线l1的表达式为( )A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )
8. 已知直线l:y=2x+4,把直线l向右平移6个单位得到直线l1 , 则直线l1的表达式为( )A、 B、 C、 D、9. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于 BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( )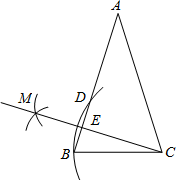 A、2 B、3 C、 D、10. A、B地相距2400米,甲、乙两人从起点A匀速步行去终点B,已知甲先出发4分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论中,其中错误的结论有( )个.
A、2 B、3 C、 D、10. A、B地相距2400米,甲、乙两人从起点A匀速步行去终点B,已知甲先出发4分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论中,其中错误的结论有( )个.
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米.
A、 B、 C、 D、二、填空题
-
11. 若代数式 有意义,则 的取值范围为.12. 若 与最简二次根式 能合并成一项,则 .13. 一次函数y=x+4的图象不经过的象限是 .14. 北京冬奥会金牌榜前十位的金牌数分别为16,12,9,8,8,8,7,7,6,5.这组数据的平均数、众数和中位数中,最大的是 .15. 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线y=x+b与△ABC有交点时,b的取值范围是 .
 16. 如图,在中,于点E,若 , 则的度数为 .
16. 如图,在中,于点E,若 , 则的度数为 . 17. 如图,△ABC中,AB=AC,CD⊥AB于D,BD=1,设BC=x,AD=y,当x>时,y关于x的函数解析式为 .
17. 如图,△ABC中,AB=AC,CD⊥AB于D,BD=1,设BC=x,AD=y,当x>时,y关于x的函数解析式为 . 18. 如图,矩形ABCD中,交CD于点E,点F在AD上,连接CF交AE于点G, , 若 , 则CD的值为 .
18. 如图,矩形ABCD中,交CD于点E,点F在AD上,连接CF交AE于点G, , 若 , 则CD的值为 .
三、解答题
-
19. 计算(1)、;(2)、 .20. 先化简,再求值: , 其中21. 某中学为了解学生参加户外活动的情况,随机调查了该校部分学生每周参加户外活动的时间,并用得到的数据绘制了如下统计图.

请根据以上信息,解答下列问题:
(1)、这次调查的学生共 ▲ 人,并补全条形统计图;(2)、求本次调查获取的样本数据的平均数、众数和中位数;(3)、若该校共有1500名学生,估计该校参加户外活动时间超过3小时的学生人数.22. 在中, , 于 .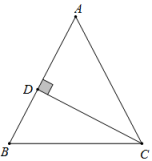 (1)、若 , 求的度数;(2)、若 , , 求的长.23. 如图,在中,过点A作于点E,于点F,且 .
(1)、若 , 求的度数;(2)、若 , , 求的长.23. 如图,在中,过点A作于点E,于点F,且 . (1)、求证:是菱形;(2)、若 , , 求菱形ABCD的面积.24. 某企业准备购买一批爱心物资捐赠给学校.经了解,若购买洗手液300瓶和口罩200包,则共需6000元;若购买洗手液500瓶和口罩300包,则共需9500元.(1)、问:每瓶洗手液和每包口罩的价格各是多少元?(2)、现计划购买洗手液和口罩,洗手液瓶数和口罩的包数之和为1000,且洗手液的瓶数不大于口罩包数的3倍.设购买洗手液m瓶,购买这两种物资的总费用为W元,请写出W(元)与m(瓶)之间的函数关系式,并求出W的最小值.25. 如图,在平面直角坐标系xOy中,直线AB:与直线CD:相交于点 , 分别交坐标轴于点A,B,C,D.
(1)、求证:是菱形;(2)、若 , , 求菱形ABCD的面积.24. 某企业准备购买一批爱心物资捐赠给学校.经了解,若购买洗手液300瓶和口罩200包,则共需6000元;若购买洗手液500瓶和口罩300包,则共需9500元.(1)、问:每瓶洗手液和每包口罩的价格各是多少元?(2)、现计划购买洗手液和口罩,洗手液瓶数和口罩的包数之和为1000,且洗手液的瓶数不大于口罩包数的3倍.设购买洗手液m瓶,购买这两种物资的总费用为W元,请写出W(元)与m(瓶)之间的函数关系式,并求出W的最小值.25. 如图,在平面直角坐标系xOy中,直线AB:与直线CD:相交于点 , 分别交坐标轴于点A,B,C,D. (1)、求a和k的值;(2)、如图,点P是直线CD上的一个动点,当的面积为20时,求点P的坐标;(3)、直线AB上有一点F,在平面直角坐标系内找一点N,使得以BF为一边,以点B,D,F,N为顶点的四边形是菱形,请直接写出符合条件的点N的坐标.26. 已知:四边形ABCD是正方形, , 点E,F,G,H分别在边AB,BC,AD,DC上.
(1)、求a和k的值;(2)、如图,点P是直线CD上的一个动点,当的面积为20时,求点P的坐标;(3)、直线AB上有一点F,在平面直角坐标系内找一点N,使得以BF为一边,以点B,D,F,N为顶点的四边形是菱形,请直接写出符合条件的点N的坐标.26. 已知:四边形ABCD是正方形, , 点E,F,G,H分别在边AB,BC,AD,DC上. (1)、如图1,若 , , 则的度数为;(2)、如图2,若 , 点E,F分別是AB,BC上的动点,求的周长;(3)、如图3,若 , GF和EH交于点O,且 , 求EH的长度.
(1)、如图1,若 , , 则的度数为;(2)、如图2,若 , 点E,F分別是AB,BC上的动点,求的周长;(3)、如图3,若 , GF和EH交于点O,且 , 求EH的长度.