辽宁省鞍山市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{1 - 2 x}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \geq 0$ B、 $x \geq \frac{1}{2}$ C、 $x \leq \frac{1}{2}$ D、 $x \leq - \frac{1}{2}$

查看试题解析
2. 以长度分别为下列各组数的线段为边，其中能构成直角三角形的是（）

A、1，2，3 B、2， $\sqrt{2}$ ， $\sqrt{3}$ C、0.6，0.8，0.9 D、2， $\frac{3}{2}$ ， $\frac{5}{2}$

查看试题解析
3. 一次函数y=kx-1经过点（-2，3），则k的值是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 为了解某校八年级学生居家体育锻炼时间，随机抽取了一个班级进行一周体育锻炼监测，每天锻炼时间记录结果如下（单位：小时）：0.4；0.7；0.5；0.5；0.8；1.2；1.0，这组数据的众数与中位数分别是（）

A、1.2；0.5 B、0.5；0.5 C、0.5；0.7 D、0.5；0.8

查看试题解析
5. 已知四边形ABCD，下面给出的四对条件不能判定它为平行四边形的是（）

A、 $A B = C D$ ， $A D ∥ B C$ B、 $A B = C D$ ， $A D = B C$ C、 $A B = C D$ ， $A B ∥ C D$ D、 $A B ∥ C D$ ， $A D ∥ B C$

查看试题解析
6. 一次函数 $y = k x + b$ 满足 $k < 0$ ， $b > 0$ ，则它的图像可能是（）

A、 B、 C、 D、

查看试题解析
7. 甲、乙、丙三名射击运动员在集训期间的测试成绩如下表所以，若需要在其中遴选一名成绩优异并稳定的运动员参加比赛，比较适合的运动员是（）
成绩/（环）
测试一
测试二
测试三
测试四
平均数
方差
甲
9.2
8.8
9.4
8.6
9.0
0.1
乙
8.8
8.6
8.7
9.1
8.8
0.035
丙
8.8
8.9
9.1
9.3
9.0
0.035

A、甲 B、乙 C、丙 D、无法确定

查看试题解析
8. 如图，两张3cm宽的纸条交叉叠放在一起，下列说法正确的是（）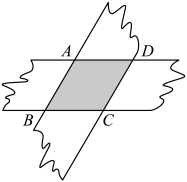

A、四边形ABCD一定是菱形 B、四边形ABCD不可能是正方形 C、四边形ABCD的面积一定是9 D、四边形ABCD的边长一定是3

查看试题解析
9. 如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形CODE的周长为（）

A、4 B、6 C、8 D、10

查看试题解析
10. 每周四下午，是八年级学生社团活动时间，小明从教学楼出发，先利用大课间时间去球场打球，然后去实验楼参加物理实验小组活动，最后回到教室写作业，已知学校的教学楼、球场以及实验楼都在一条直线上，小明与教学楼的距离y（米）与离开教学楼的时间x（分）之间的函数关系如图所示，则下列说法正确的是（）

A、小明打球的时间是35分钟 B、实验楼距离球场30米 C、实验楼距离教学楼40米 D、社团活动时间是1小时

查看试题解析

二、填空题

11. 计算： $(2 + \sqrt{3}) (2 - \sqrt{3}) =$ ．

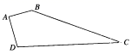
查看试题解析
12. 如图，有一四边形空地ABCD，AB⊥AD，AB＝3，AD＝4，BC＝12，CD＝13，则四边形ABCD的面积为.

查看试题解析
13. 某班共有40名学生，平均身高168cm，其中24名男生平均身高170cm，那么16名女生的平均身高是cm．

查看试题解析
14. 如果直线 $y = k_{1} x + b_{1}$ 和直线 $y = k_{2} x + b_{2} (k_{1} > k_{2} > 0)$ 的交点坐标为 $(- 3 ， 2)$ ，则不等式 $k_{1} x + b_{1} < k_{2} x + b_{2}$ 的解集是．

查看试题解析
15. 如图，CD，BE是 $△ A B C$ 的高，点P是BC边的中点，连接DP，EP，若 $D P = 3$ ，则EP的长是．

查看试题解析
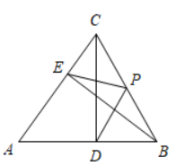16. 如图，矩形ABCD中，AB=10，AD=6，点M是边CD上的动点，连接BM，AM，若△AMB是等腰三角形，则AM的长是．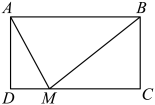

查看试题解析

三、解答题

17. 计算

(1)、 $(\sqrt{45} + \sqrt{18}) - 2 (\sqrt{8} - \sqrt{125})$ ；

(2)、 $(2 \sqrt{48} - 3 \sqrt{27}) \div 6$ ．

查看试题解析
18. 如图，点O是位于东西海岸线的一个港口，A，B两艘客轮从港口O同时出发，A客轮沿北偏东75°航行，航速是每小时18海里，B客轮沿北偏西15°方向航行，航速是每小时24海里，请计算3小时之后两客轮之间的距离．

查看试题解析
19. 在正方形ABCD中，点E，F分别是BC，AB边上的点，连接AE，过点F作FG⊥AE交AE于点G，交DC于点H，试猜想FH与AE的数量关系，并证明你的结论．

查看试题解析
20. 某学校开展“读书节”活动，为了解学生每周的课外阅读时间情况，随机调查了部分学生，对被抽查学生每周的课外阅读时间x（单位：时）进行分组整理，并绘制了如图所示不完整的频数分布表和频数分布直方图．
阅读时间/时
组中值
频数
百分比
$0 \leq x < 2$
1
10
10%
$2 \leq x < 4$
3
21
21%
$4 \leq x < 6$
5
40
40%
$6 \leq x < 8$
7
$8 \leq x \leq 10$
9
4
4%
根据图中提供的信息，解答下列问题：

(1)、本次共随机调查了名学生；

(2)、请补全频数分布直方图；

(3)、估计该学校学生每周平均课外阅读时间；

(4)、请估计该校1000名学生中每周的课外阅读时间不小于6时的人数．

查看试题解析
21. 某工厂新开发一种电子产品，市场统一销售价20元/件，产品上市两周迎来热销，从第3周开始价格开始上涨，预计每周将上涨5元，若物价局规定其销售价不能超过50元．

(1)、请求出销售价y（元）与时间第x（周）之间的函数关系式，并直接写出自变量x的取值范围；

(2)、某公司在产品上市后第5周时到商场进行采购，采购时恰好赶上购物节促销活动，甲商场对该电子产品打八折，乙商场规定：超过20件以后该产品打七折，若该采购员需要购买50件这种电子产品，选择哪个商场比较合算．

查看试题解析
22. 如图，一次函数 $y = x + 2$ 与x轴，y轴分别交于点A，B，点 $M (1 ， m)$ 是直线AB上一点，直线MC交x轴于点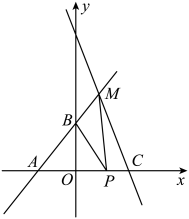 $C (\frac{5}{2} ， 0)$ ；

(1)、求直线MC的函数解析式；

(2)、若点P是线段AC上一动点，连接BP，MP，若 $△ A B P$ 的面积是 $△ M P C$ 面积的2倍，求P点坐标．

查看试题解析
23. 如图①，已知菱形ABCD的边长为2cm， $∠ A B C = 60 °$ ，点M从点D开始向点C以1cm/s的速度运动，同时点N从点C开始以相同的速度向点B运动，连接AM，AN，MN，设运动时间为xs；

(1)、试判断 $△ A M N$ 的形状，请说明理由；

(2)、当x为多少时，点A到MN的距离h最小？请直接写出满足条件的x和h的值；

(3)、在（2）的条件下，连接对角线AC，BD交于点O，在图②画出图形并判断以O，N，M，D为顶点的四边形的形状，请说明理由．

查看试题解析

成绩/（环）	测试一	测试二	测试三	测试四	平均数	方差
甲	9.2	8.8	9.4	8.6	9.0	0.1
乙	8.8	8.6	8.7	9.1	8.8	0.035
丙	8.8	8.9	9.1	9.3	9.0	0.035

阅读时间/时	组中值	频数	百分比
$0 \leq x < 2$	1	10	10%
$2 \leq x < 4$	3	21	21%
$4 \leq x < 6$	5	40	40%
$6 \leq x < 8$	7
$8 \leq x \leq 10$	9	4	4%