江西省宜春市高安市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 的相反数是( )A、﹣ B、 C、 D、32. 如图,△OAB为直角三角形,OA=5,AB=4,则点A的坐标为( )
 A、(4,5) B、(4,3) C、(3,4) D、(3,5)3. 如图,矩形ABCD的对角线AC=8,∠BOC=120°,则AB的长为( )
A、(4,5) B、(4,3) C、(3,4) D、(3,5)3. 如图,矩形ABCD的对角线AC=8,∠BOC=120°,则AB的长为( )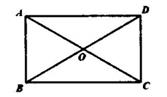 A、3 B、4 C、5 D、64. 下列关于一次函数y=﹣2x+2的图象的说法中,错误的是( )A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为(2,0) C、当x>0时,y<2 D、y的值随着x值的增大而减小5. 如图,直线y=2x和y=kx+b相交于点P (2,4),则不等式2x≤kx+b的解集为( )
A、3 B、4 C、5 D、64. 下列关于一次函数y=﹣2x+2的图象的说法中,错误的是( )A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为(2,0) C、当x>0时,y<2 D、y的值随着x值的增大而减小5. 如图,直线y=2x和y=kx+b相交于点P (2,4),则不等式2x≤kx+b的解集为( )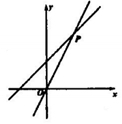 A、x≥4 B、x≤4 C、x≥2 D、x≤26. 一组数据:的平均数为 , 众数为 , 中位数为 , 则以下判断正确的是( )A、一定出现在中 B、一定出现在中 C、一定出现在中 D、 , , 都不会出现在中
A、x≥4 B、x≤4 C、x≥2 D、x≤26. 一组数据:的平均数为 , 众数为 , 中位数为 , 则以下判断正确的是( )A、一定出现在中 B、一定出现在中 C、一定出现在中 D、 , , 都不会出现在中二、填空题
-
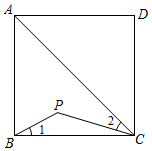
7. 化简: = .8. 把函数的图象向下平移3个单位长度,得到的函数图象的解析式为 .9. 如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为°.
 10. 南吕是国家历史文化名城,其名源于“昌大南疆,南方昌盛”之意,市内的滕王阁、八一起义纪念馆、海昏候遗址、绳金塔、八大山人纪念馆等都有深厚的文化底蕴.某班同学分小组到以上五个地方进行研学,人数分别为:12,5,11,5,7(单位:人),这组数据的中位数是 .11. 如图,两条宽度分别为2和4的长方形纸条交叉放置,重叠部分为四边形 , 若 , 则四边形的面积是
10. 南吕是国家历史文化名城,其名源于“昌大南疆,南方昌盛”之意,市内的滕王阁、八一起义纪念馆、海昏候遗址、绳金塔、八大山人纪念馆等都有深厚的文化底蕴.某班同学分小组到以上五个地方进行研学,人数分别为:12,5,11,5,7(单位:人),这组数据的中位数是 .11. 如图,两条宽度分别为2和4的长方形纸条交叉放置,重叠部分为四边形 , 若 , 则四边形的面积是 12. 如图,在中,已知: , , , 动点从点出发,沿射线以1cm/s的速度运动,设运动的时间为秒,连接 , 当为等腰三角形时,的值为 .
12. 如图,在中,已知: , , , 动点从点出发,沿射线以1cm/s的速度运动,设运动的时间为秒,连接 , 当为等腰三角形时,的值为 .
三、解答题
-
13.14. 如图,点C为线段AB上一点且不与A,B两点重合,分别以AC,BC为边向AB的同侧做角为60°的菱形.请仅用无刻度的直尺分别按下列要求作图.(保留作图痕迹).(1)、在图1中,连接DF,若AC=BC,作出线段DF的中点M;
 (2)、在图2中,连接DF,若 , 作出线段DF的中点N.
(2)、在图2中,连接DF,若 , 作出线段DF的中点N.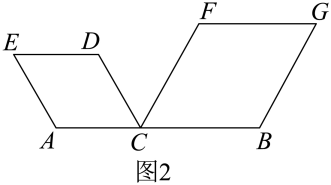 15. 如图, , 平分∠ABC交 于点D,点C在 上且 ,连接 .求证:四边形 是菱形.
15. 如图, , 平分∠ABC交 于点D,点C在 上且 ,连接 .求证:四边形 是菱形. 16. 某种子站销售一种玉米种子,单价为5元千克,为惠民促销,推出以下销售方案:付款金额(元)与购买种子数量(千克)之间的函数关系如图所示.
16. 某种子站销售一种玉米种子,单价为5元千克,为惠民促销,推出以下销售方案:付款金额(元)与购买种子数量(千克)之间的函数关系如图所示. (1)、当时,求与之间的的函数关系式:(2)、徐大爷付款20元能购买这种玉米种子多少千克?17. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点 和点 距离门槛 都为1尺(1尺=10寸),则 的长是多少?
(1)、当时,求与之间的的函数关系式:(2)、徐大爷付款20元能购买这种玉米种子多少千克?17. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点 和点 距离门槛 都为1尺(1尺=10寸),则 的长是多少?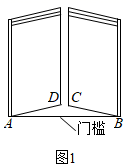
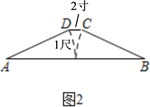 18. 某校八年级学生开展踢键子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
18. 某校八年级学生开展踢键子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):1号
2号
3号
4号
5号
总数
甲班
120
118
130
109
123
600
乙班
109
120
115
139
117
600
经统计发现两班总数相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)、填空:甲班的优秀率为 , 乙班的优秀率为;(2)、填空:甲班比赛数据的中位数为 , 乙班比赛数据的中位数为;(3)、根据以上两条信息,你认为应该把冠军奖杯发给哪一个班级?简述你的理由.19. 如图,的对角线与相交于点O , 过点B作BPAC , 过点C作CPBD , 与相交于点P . (1)、试判断四边形的形状,并说明理由;(2)、若将改为矩形 , 且 , 其他条件不变,求四边形的面积;(3)、要得到矩形 , 应满足的条件是(填上一个即可).20. 定义:关于x的一次函数y=ax+b与y=bx+a(ab≠0)叫做一对交换函数,例如:一次函数y=3x+4与y=4x+3就是一对交换函数.(1)、一次函数y=2x﹣b的交换函数是;(2)、当b≠﹣2时,(1)中两个函数图象交点的横坐标是;(3)、若(1)中两个函数图象与y轴围成的三角形的面积为4,求b的值.21. 已知:如图一次函数与轴相交于点 , 与轴相交于点 , 这两个函数图象相交于点 .
(1)、试判断四边形的形状,并说明理由;(2)、若将改为矩形 , 且 , 其他条件不变,求四边形的面积;(3)、要得到矩形 , 应满足的条件是(填上一个即可).20. 定义:关于x的一次函数y=ax+b与y=bx+a(ab≠0)叫做一对交换函数,例如:一次函数y=3x+4与y=4x+3就是一对交换函数.(1)、一次函数y=2x﹣b的交换函数是;(2)、当b≠﹣2时,(1)中两个函数图象交点的横坐标是;(3)、若(1)中两个函数图象与y轴围成的三角形的面积为4,求b的值.21. 已知:如图一次函数与轴相交于点 , 与轴相交于点 , 这两个函数图象相交于点 .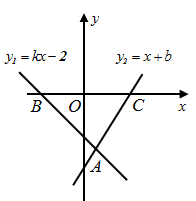 (1)、求出 , 的值和点的坐标;(2)、连接 , 直线上是否存在一点 , 使.如果存在,求出点的坐标;(3)、结合图象,直接写出时的取值范围.22. 如图,在平面直角坐标系中,直线与坐标轴相交于点和 , 点从点出发沿方向以每秒4个单位长度的速度向点匀速运动,同时点从点出发沿方向以每秒2个单位长度的速度向点匀速运动,设点、时间是秒().过点作于点 , 连接 , .
(1)、求出 , 的值和点的坐标;(2)、连接 , 直线上是否存在一点 , 使.如果存在,求出点的坐标;(3)、结合图象,直接写出时的取值范围.22. 如图,在平面直角坐标系中,直线与坐标轴相交于点和 , 点从点出发沿方向以每秒4个单位长度的速度向点匀速运动,同时点从点出发沿方向以每秒2个单位长度的速度向点匀速运动,设点、时间是秒().过点作于点 , 连接 , .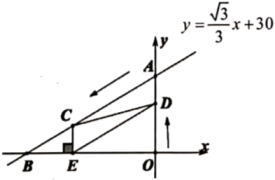 (1)、求 , 和;(2)、求证:四边形是平行四边形;(3)、当为何值时,四边形为 矩形?说明理由.23. 如图1,在 和 中,顶点 是它们的公共顶点, , .
(1)、求 , 和;(2)、求证:四边形是平行四边形;(3)、当为何值时,四边形为 矩形?说明理由.23. 如图1,在 和 中,顶点 是它们的公共顶点, , .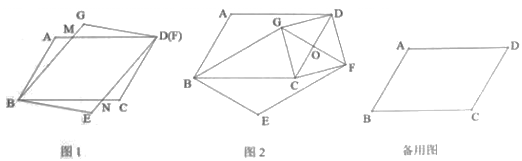 (1)、(特例感悟)当顶点 与顶点 重合时(如图1), 与 相交于点 , 与 相交于点 ,求证:四边形 是菱形;(2)、(探索论证)如图2,当 时,四边形 是什么特殊四边形?试证明你的结论;(3)、(拓展应用)试探究:当 等于多少度时,以点 为顶点的四边形是矩形?请给予证明.
(1)、(特例感悟)当顶点 与顶点 重合时(如图1), 与 相交于点 , 与 相交于点 ,求证:四边形 是菱形;(2)、(探索论证)如图2,当 时,四边形 是什么特殊四边形?试证明你的结论;(3)、(拓展应用)试探究:当 等于多少度时,以点 为顶点的四边形是矩形?请给予证明.