江西省吉安市泰和县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 将点A向左平移3个单位,再向上平移4个单位得到点B,则点B的坐标是( )A、(-5,-7) B、(-5,1) C、(1,1) D、(1,-7)4. 一个正多边形,它的每一个外角都等于40°,则该正多边形是( )A、正六边形
2. 下列说法错误的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则3. 将点A向左平移3个单位,再向上平移4个单位得到点B,则点B的坐标是( )A、(-5,-7) B、(-5,1) C、(1,1) D、(1,-7)4. 一个正多边形,它的每一个外角都等于40°,则该正多边形是( )A、正六边形 B、正七边形
B、正七边形 C、正八边形
C、正八边形 D、正九边形
5. 数形结合是解决数学问题常用的思想方法.如图,直线 与直线 相交于点 .根据图象可知,关于x的不等式 的解集是( )
D、正九边形
5. 数形结合是解决数学问题常用的思想方法.如图,直线 与直线 相交于点 .根据图象可知,关于x的不等式 的解集是( ) A、 B、 C、 D、6. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( )
A、 B、 C、 D、6. 如图,点P为定角∠AOB平分线上的一个定点,且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON的值不变;③MN的长不变;④四边形PMON的面积不变,其中,正确结论的是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
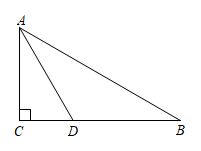
7. 若分式的值为0,则x=.8. 如图,在中, , 平分 , 与边交于点 , , 若点到的距离等于5cm,则的长为 cm.
 9. 如图,在实数范围内规定新运算“△”,其规则是:a△b=2a﹣b.已知不等式x△k≥1的解集在数轴上,则k的值是 .
9. 如图,在实数范围内规定新运算“△”,其规则是:a△b=2a﹣b.已知不等式x△k≥1的解集在数轴上,则k的值是 . 10. 若关于 的方程 产生增根,则 .11. 如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=6cm,MC=4cm,则阴影部分的面积是cm2 .
10. 若关于 的方程 产生增根,则 .11. 如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=6cm,MC=4cm,则阴影部分的面积是cm2 . 12. 如图,在中, , , 点P在边上以的速度从点A向点D运动,点Q在边上以的速度从点C出发,在间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止运动).设运动(其中)时,以P、D、Q、B四点组成的四边形是平行四边形,则t的所有可能取值为 .
12. 如图,在中, , , 点P在边上以的速度从点A向点D运动,点Q在边上以的速度从点C出发,在间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止运动).设运动(其中)时,以P、D、Q、B四点组成的四边形是平行四边形,则t的所有可能取值为 .
三、解答题
-
13. 分解因式及解方程:(1)、(2)、14. 解不等式组 , 并把不等式组的解集表示在数轴上.
 15. 先化简,再求值:()÷ , 然后从﹣1,1,3中选择适当的数代入求值.16. 如图,7×7的网格中,A,B,C均在格点上,请用无刻度的直尺作图(保留作图痕迹,不写作法)
15. 先化简,再求值:()÷ , 然后从﹣1,1,3中选择适当的数代入求值.16. 如图,7×7的网格中,A,B,C均在格点上,请用无刻度的直尺作图(保留作图痕迹,不写作法)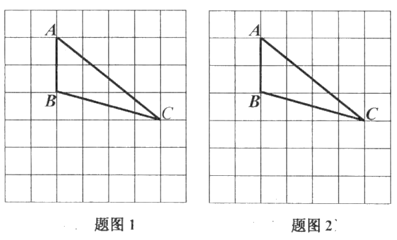 (1)、在图1中找一格点D,使得△ACD为等腰三角形(找到一个即可);(2)、在图2中作出∠BAC的角平分线。17. 如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=AC=8,若 , 求DE的长.
(1)、在图1中找一格点D,使得△ACD为等腰三角形(找到一个即可);(2)、在图2中作出∠BAC的角平分线。17. 如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=AC=8,若 , 求DE的长. 18. 如图, ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.
18. 如图, ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.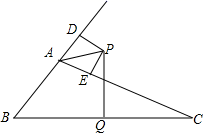 (1)、求证:BD=CE;(2)、若AB=6cm,AC=10cm,求AD的长.19. 虹桥中学为了创建良好的校园读书环境,去年购买了一批图书.其中故事书的单价比文学书的单价多4元,用1200元购买的故事书与用800元购买的文学书数量相等.(1)、求去年购买的文学书和故事书的单价各是多少元?(2)、若今年文学书的单价比去年提高了 ,故事书的单价与去年相同,这所中学今年计划再购买文学书和故事书共200本,且购买文学书和故事书的总费用不超过2120元,这所中学今年至少要购买多少本文学书?20. 如图,在平行四边形中, , 将纸片沿对角线对折,边与边交于点E,此时,恰为等边三角形.
(1)、求证:BD=CE;(2)、若AB=6cm,AC=10cm,求AD的长.19. 虹桥中学为了创建良好的校园读书环境,去年购买了一批图书.其中故事书的单价比文学书的单价多4元,用1200元购买的故事书与用800元购买的文学书数量相等.(1)、求去年购买的文学书和故事书的单价各是多少元?(2)、若今年文学书的单价比去年提高了 ,故事书的单价与去年相同,这所中学今年计划再购买文学书和故事书共200本,且购买文学书和故事书的总费用不超过2120元,这所中学今年至少要购买多少本文学书?20. 如图,在平行四边形中, , 将纸片沿对角线对折,边与边交于点E,此时,恰为等边三角形.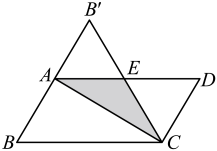 (1)、猜想与的位置关系,并证明你的结论;(2)、连接 , 请说明四边形为平行四边形;21. 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
(1)、猜想与的位置关系,并证明你的结论;(2)、连接 , 请说明四边形为平行四边形;21. 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n), (1)、求n,k ,b的值;(2)、若函数y=kx+b的函数值大于函数y=x+1的函数值,则x的取值范围是多少?(3)、求四边形AOCD的面积;22. 阅读下面材料,解答后面的问题.
(1)、求n,k ,b的值;(2)、若函数y=kx+b的函数值大于函数y=x+1的函数值,则x的取值范围是多少?(3)、求四边形AOCD的面积;22. 阅读下面材料,解答后面的问题.解方程: - =0.
解:设y= ,则原方程可化为y- =0,方程两边同时乘y , 得y2-4=0,解得y1=2,y2=-2.
经检验,y1=2,y2=-2都是方程y- =0的解.
当y=2时, =2,解得x=-1;当y=-2时, =-2,解得x= .
经检验,x1=-1,x2= 都是原分式方程的解.所以原分式方程的解为x1=-1,x2= .
上述这种解分式方程的方法称为换元法.
问题:
(1)、若在方程 - =0中,设y= ,则原方程可化为;(2)、若在方程 - =0中,设y= ,则原方程可化为;(3)、模仿上述换元法解方程: - -1=0.23. 通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整.
原题:如图1,点E、F分别在正方形的边、上, , 连接 , 试猜想、、之间的数量关系.
(1)、思路梳理把绕点A逆时针旋转90°至 , 可使与重合,由 , 得 , 即点F、D、G共线,易证 , 故、、之间的数量关系为 . (要求写出必要的推理过程)
(2)、类比引申如图2,点E、F分别在正方形的边、的延长线上, , 连接 , 试猜想、、之间的数量关系为 , 并给出证明.
(3)、联想拓展如图3,在中, , , 点D、E均在边上,且 , 若 , , 求的长.