吉林省长春市南关区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
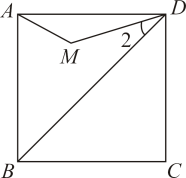
1. 若分式在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、2. 一个纳米粒子的直径是35纳米(1纳米米),用科学记数法表示为( )A、米 B、米 C、米 D、米3. 在正比例函数中,y的值随着x值的增大而减小,则点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,中,的平分线与相交于点E,若 , 则的值为( )
 A、6 B、8 C、12 D、185. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A、6 B、8 C、12 D、185. 如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( ) A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形6. 某校11名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前5名,则他不仅要知道自己的成绩,还应知道这11名学生成绩的( )A、平均数 B、众数 C、方差 D、中位数7. 反比例函数的图像的两个分支分别位于第二、四象限,则一次函数的图像大致是( )A、
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形→菱形→矩形 D、平行四边形→菱形→正方形→矩形6. 某校11名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前5名,则他不仅要知道自己的成绩,还应知道这11名学生成绩的( )A、平均数 B、众数 C、方差 D、中位数7. 反比例函数的图像的两个分支分别位于第二、四象限,则一次函数的图像大致是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数的图象与大正方形的一边交于第一象限的点 , 且经过小正方形的顶点B,则阴影部分的面积是( )
8. 如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数的图象与大正方形的一边交于第一象限的点 , 且经过小正方形的顶点B,则阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、解答题
-
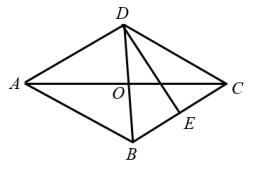
9. 计算: .10. 先化简,再求值: , 其中 .11. 为保障新冠病毒抗原检测试剂盒的需求,某生物科技公司开启“加速”模式生产效率比原先提高了20%,现在生产480万试剂盒所用的时间比原先生产450万试剂盒所用的时间少1天.问原先每天生产多少万试剂盒?12. 如图,菱形的对角线相交于点O,垂直平分 , 垂足为点E,求的大小.
 13. 如图,图①、图②、图③均是的正方形网格,小正方形的边长为1,每个小正方形的顶点称为格点,线段的端点均在格点上.只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,所画图形不全等,不要求写出画法
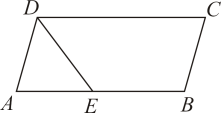
13. 如图,图①、图②、图③均是的正方形网格,小正方形的边长为1,每个小正方形的顶点称为格点,线段的端点均在格点上.只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,所画图形不全等,不要求写出画法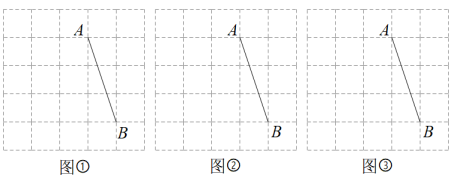 (1)、在图①中以线段为边画一个正方形 .(2)、在图②中以线段为边画一个菱形 .(3)、在图③中以A,B为顶点画一个平行四边形.14. 如图,点C是的中点,四边形是平行四边形, .
(1)、在图①中以线段为边画一个正方形 .(2)、在图②中以线段为边画一个菱形 .(3)、在图③中以A,B为顶点画一个平行四边形.14. 如图,点C是的中点,四边形是平行四边形, . (1)、求证:四边形是矩形.(2)、若 , 求四边形的周长.15. 某校将学生体能测试成绩分为A、B、C、D四个等级,依次记为4分、3分、2分、1分.为了解学生整体体能状况,随机抽取部分学生的测试成绩进行统计并绘制了不完整的统计图①和图②.
(1)、求证:四边形是矩形.(2)、若 , 求四边形的周长.15. 某校将学生体能测试成绩分为A、B、C、D四个等级,依次记为4分、3分、2分、1分.为了解学生整体体能状况,随机抽取部分学生的测试成绩进行统计并绘制了不完整的统计图①和图②.等级
频数
频率
A
50
m
B
90
0.45
C
n
0.20
D
20
0.10
图①
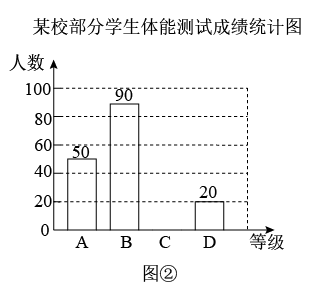
请根据图中的信息,解答下列问题:
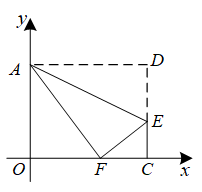
(1)、本次抽取的学生共人,m的值为 , n的值为 .(2)、补全条形统计图.(3)、求被抽取学生测试成绩的平均数、中位数和众数.16. 如图,在平面直角坐标系中,直线与双曲线相交于、两点. (1)、求对应的函数表达式.(2)、过点B作轴于点P,求的面积.(3)、根据函数图象,直接写出关于x的不等式的解集.17. 如图,将矩形纸片折叠,使点C刚好落在线段上,且折痕分别与边相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边、相交于点E、F.
(1)、求对应的函数表达式.(2)、过点B作轴于点P,求的面积.(3)、根据函数图象,直接写出关于x的不等式的解集.17. 如图,将矩形纸片折叠,使点C刚好落在线段上,且折痕分别与边相交,设折叠后点C、D的对应点分别为点G、H,折痕分别与边、相交于点E、F.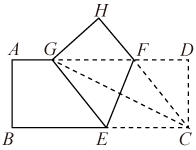 (1)、判断四边形的形状,并证明你的结论.(2)、若 , 当最大时,求四边形的面积.18. 张华公司、家、火车站在同一条直线上,张华开车匀速从家到火车站接客户,接到客户后,再以相同的速度原路返回公司(等灯时间忽略不计),张华离公司的距离与他所用的时间的函数关系如图所示.
(1)、判断四边形的形状,并证明你的结论.(2)、若 , 当最大时,求四边形的面积.18. 张华公司、家、火车站在同一条直线上,张华开车匀速从家到火车站接客户,接到客户后,再以相同的速度原路返回公司(等灯时间忽略不计),张华离公司的距离与他所用的时间的函数关系如图所示. (1)、张华公司与家的距离为 , 张华开车的速度为 .(2)、求张华从火车站返回公司的过程中,y与x的函数关系式.(3)、张华开车出发多长时间,他距离公司?19. 阅读理解:
(1)、张华公司与家的距离为 , 张华开车的速度为 .(2)、求张华从火车站返回公司的过程中,y与x的函数关系式.(3)、张华开车出发多长时间,他距离公司?19. 阅读理解:在平面直角坐标系中,点P的坐标为 , 点Q的坐标为 , 且 , 若P、Q为某矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为P、Q的“相关矩形”,如图①中的矩形为点P、Q的“相关矩形”.
 (1)、已知点A的坐标为
(1)、已知点A的坐标为①若点B的坐标为 , 则点A、B的“相关矩形”的周长为 ▲ .
②若点C在直线上,且点A、C的“相关矩形”为正方形,求直线的解析式.
(2)、已知点M的坐标为 , 点N的坐标为 , 若使函数的图象与点M、N的“相关矩形”有两个公共点,直接写出k的取值范围.三、填空题
-
20. .21. 已知池中有的水,每小时抽 , 则剩余水的体积与时间的函数关系式是 . (写出自变量取值范围)22. 已知点在反比例函数的图像上,则 . (填“>”、“<”或“=”)