吉林省长春市德惠市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{1}{x - 3}$ 有意义，x应满足的条件是（）

A、x＞3 B、x=3 C、x＜3 D、x≠3

查看试题解析
2. 成年人手上大拇指指盖的面积约为1平方厘米，若以平方米为单位进行估算，其面积为（）

A、 $1 0^{- 4}$ B、 $1 0^{- 3}$ C、 $1^{- 4}$ D、 $1^{- 3}$

查看试题解析
3. 某气象台为了预报台风，首先需要确定台风中心的位置，则下列说法能确定台风中心位置的是（）

A、北纬38° B、距气象台500海里 C、海南附近 D、北纬38°，东经136°

查看试题解析
4. 在端午节到来之前，儿童福利院对全体小朋友爱吃哪几种粽子作调查，以决定最终买哪种粽子．下面的调查数据中最值得关注的是（）

A、方差 B、平均数 C、中位数 D、众数

查看试题解析
5. 点 $P (2 - a ， 2 a - 1)$ 在第四象限，且到 $y$ 轴的距离为3，则 $a$ 的值为（）

A、 $- 1$ B、 $- 2$ C、1 D、2

查看试题解析
6. 如图，在四边形 $A B C D$ 中，AB∥CD，添加下列一个条件后，一定能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $A B = B C$ B、 $A D = B C$ C、 $∠ A = ∠ C$ D、 $∠ B + C = 180 °$

查看试题解析
7. 已知小林的家、体育场、文具店在同一直线上，图中的信息反映的过程：小林从家跑步去体育场，在体育场锻炼了一阵后又走到文具店买笔，然后再走回家，图中x表示时间，y表示小林离家的距离，依据图中的信息，下列说法错误的是（）

A、体育场离小林家2.5km B、小林在文具店买笔停留了20min C、小林从体育场出发到文具店的平均速度是50m/min D、小林从文具店回家的平均速度是60m/min

查看试题解析
8. 如图，A、B是反比例函数 $y = \frac{6}{x}$ 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和3．则 $△ O A B$ 的面积是（）

A、2 B、2.5 C、3 D、6

查看试题解析

二、填空题

9. 已知平行四边形 $A B C D$ 中， $∠ A$ 比 $∠ B$ 小40°，那么 $∠ C$ 的度数是．

查看试题解析
10. 若点 $A (- 1 ， y_{1}) ， B (2 ， y_{2}) ， C (3 ， y_{3})$ 在反比例函数 $y = - \frac{6}{x}$ 的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（用“>”连接）．

查看试题解析
11. 已知一组数据：2，5，5，6，7，则这组数据的方差是

查看试题解析
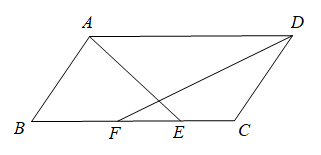12. 如图，平行四边形 $A B C D$ 中， $A B = 4 ， A D = 6 ， ∠ B A D$ 和 $∠ A D C$ 的平分线交 $B C$ 于E、F两点，则 $E F$ 的长是．

查看试题解析
13. 如图所示，点O为▱ABCD内一点，连接BD，OA，OB，OC，OD，已知△BCO的面积为3，△ABO的面积为5 $\sqrt{3}$ ，则阴影部分的面积是．

查看试题解析
14. 如图，在Rt△ABC中，∠BAC＝90°，且BA＝6，AC＝8，点D是斜边BC上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为.

查看试题解析

三、解答题

15. 先化简，再求值： $(\frac{1}{x - 2} - \frac{1}{x + 1}) \cdot \frac{x^{2} - 1}{3}$ ，其中 $x = 3$ ．

查看试题解析
16. 解分式方程： $\frac{x}{2 x + 1} = \frac{1}{3}$ ．

查看试题解析
17. 已知正比例函数y=ax与反比例函数 $y = \frac{b}{x}$ 的图象有一个公共点A（1，2）．

(1)、求这两个函数的表达式；

(2)、画出草图，根据图象写出正比例函数值大于反比例函数值时x的取值范围．

查看试题解析
18. 如图，在正方形ABCD中，点P在对角线BD上，PE⊥BC，PF⊥CD，垂足分别为E、F．求证：AP=EF．

查看试题解析
19. 如图，菱形ABCD的对角线相交于点O，∠BAD＝60°，菱形ABCD的周长为24．

(1)、求对角线BD的长；

(2)、求菱形ABCD的面积．

查看试题解析
20. 21世纪已经进入了中国太空时代，2021年到2022年，我国会通过11次航天发射完成空间站建设，空间站有“天和”核心舱、“问天”和“梦天”两个实验舱，我国空间站的建成将为开展太空实验及更广泛的国际合作提供精彩舞台校团委以此为契机，组织了“中国梦，航天情”系列活动．下面是八年级甲、乙两个班各项目的成绩（单位：分）：
项目班次
知识竞赛
演讲比赛
版面创作
甲
85
91
88
乙
90
84
87

(1)、如果根据三项成绩的平均分计算最后成绩，请通过计算说明甲、乙两班谁将获胜；

(2)、如果将知识竞赛、演讲比赛、版面创作按5：3：2的比例确定最后成绩，请通过计算说明甲、乙两班谁将获胜．

查看试题解析
21. 某校为了改善学生伙食，准备午餐为学生提供鸡腿．现有A、B两家副食品厂可以提供规格为 $75 g$ 的鸡腿，而且它们的价格相同，品质也相近．质检人员分别从两家随机各抽取10个，记录它们的质量（单位：g）如下：
A加工厂 74 74 74 75 73 77 78 72 76 77
B加工厂 78 74 77 73 75 75 74 74 75 75
并对以上数据进行整理如下：

平均数
中位数
众数
方差
A加工厂
75
74.5
b
3.4
B加工厂
75
a
75
2
根据以上分析，回答下列问题：

(1)、统计表中a= ， b=；

(2)、根据以上信息估计B加工厂加工的100个鸡腿中，质量为 $75 g$ 的鸡腿有多少个？

(3)、如果考虑鸡腿的规格，学校应该选购哪家加工厂的鸡腿？说明理由．

查看试题解析
22. 已知：如图，在平行四边形 $A B C D$ 中，G、H分别是 $A D$ 、 $B C$ 的中点，E、O、F分别是对角线 $B D$ 上的四等分点，顺次连接G、E、H、F.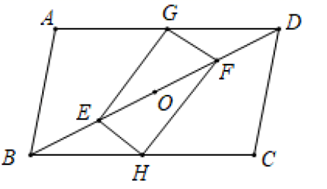

(1)、求证：四边形 $G E H F$ 是平行四边形；

(2)、当平行四边形 $A B C D$ 满足条件时，四边形 $G E H F$ 是菱形；

(3)、若 $B D = 2 A B$ ，探究四边形 $G E H F$ 的形状，并说明理由.

查看试题解析
23. 如图，直线 $M N$ 与x轴、y轴分别相交于A、C两点，过A、C两点分别作x轴、y轴的垂线相交于点 $B (8 ， 6)$ ．

(1)、直线 $M N$ 的函数表达式是．

(2)、动点P从O出发，以每秒1个单位的速度沿x轴的正半轴匀速运动，运动时间为t秒， $△ A B P$ 的面积为S，求S与t的函数表达式；

(3)、在（2）的条件下，当 $t = 4$ 时，在平面内是否存在一点Q，使得以A、C、P、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析

项目班次	知识竞赛	演讲比赛	版面创作
甲	85	91	88
乙	90	84	87

	平均数	中位数	众数	方差
A加工厂	75	74.5	b	3.4
B加工厂	75	a	75	2