吉林省松原市乾安县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下列四组数,可作为直角三角形三边长的是( )A、 、 、 B、 、 、 C、 、 、 D、 、 、3. 不能判定四边形为平行四边形的题设是( )
 A、 , B、 , C、 , D、 ,4. 下列表示y与x之间的关系的图象中,y不是x的函数的是( )A、
A、 , B、 , C、 , D、 ,4. 下列表示y与x之间的关系的图象中,y不是x的函数的是( )A、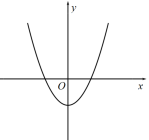 B、
B、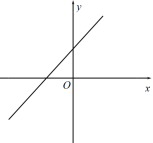 C、
C、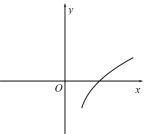 D、
D、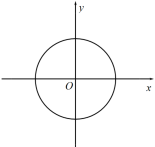 5. 甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )
5. 甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )统计量
甲
乙
丙
丁
平均数
方差
A、甲 B、乙 C、丙 D、丁6. 如图,一个长方体铁块放置在圆柱形水槽容器内,向容器内按一定的速度均匀注水,60秒后将容器内注满.容器内水面的高度h(cm)与注水时间t(s)之间的函数关系图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
7. 函数中,自变量x的取值范围是 .8. 已知一个样本1,2,3,x,5的平均数是3,则这个样本的方差是 .
9. 若正比例函数y=kx(k是常数,k≠0)的图象经过第一、三象限,请写出一个满足上述要求的k的值 .10. 如图,每个小正方形的边长都相等, , , 是小正方形的顶点,则的度数为 .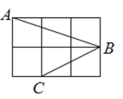 11. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=cm.
11. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=cm.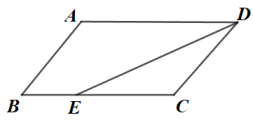 12. 直角三角形两直角边长分别为5cm和12cm,则斜边上的中线长为cm.13. 函数的图像如图所示,则关于x的不等式的解集是 .
12. 直角三角形两直角边长分别为5cm和12cm,则斜边上的中线长为cm.13. 函数的图像如图所示,则关于x的不等式的解集是 .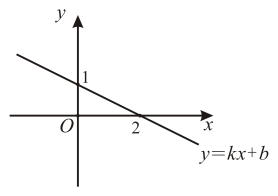 14. 如图,在矩形ABCD中,AC是对角线.将矩形ABCD绕点B顺时针旋转90°到矩形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为 .
14. 如图,在矩形ABCD中,AC是对角线.将矩形ABCD绕点B顺时针旋转90°到矩形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为 .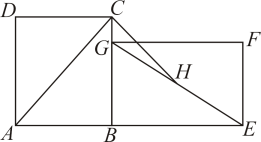
三、解答题
-
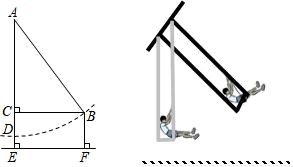
15. 计算: .16. 已知 .(1)、 满足什么条件时, 是一次函数?(2)、 满足什么条件时, 是正比例函数?17. 如图,有一架秋千,当它静止时,踏板离地的垂直高度DE=1m,将它往前推送4m(水平距离BC=4m)时,秋千的踏板离地的垂直高度BF=2m,秋千的绳索始终拉得很直,求绳索AD的长度.
 18. 如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且AE=CF,连接BE,DF.求证:BE=DF.
18. 如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且AE=CF,连接BE,DF.求证:BE=DF.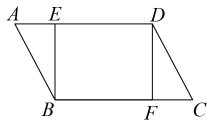 19. 如图,网格中有一条线段AB,点A、B都在格点上,网格中的每个小正方形的边长为1.请在图①和图②中各画出一个格点ABC,使ABC是直角三角形,且∠ACB=90°,并满足以下要求:
19. 如图,网格中有一条线段AB,点A、B都在格点上,网格中的每个小正方形的边长为1.请在图①和图②中各画出一个格点ABC,使ABC是直角三角形,且∠ACB=90°,并满足以下要求: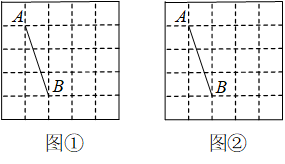 (1)、在图①中画出的三角形的两条直角边的长度均为有理数(画出一个即可);(2)、在图②中画出的三角形的两条直角边的长度均为无理数(画出一个即可).20. 已知矩形ABCD中,对角线AC与BD相交于点O.分别过点D、C作AC、BD的平行线交于点E.
(1)、在图①中画出的三角形的两条直角边的长度均为有理数(画出一个即可);(2)、在图②中画出的三角形的两条直角边的长度均为无理数(画出一个即可).20. 已知矩形ABCD中,对角线AC与BD相交于点O.分别过点D、C作AC、BD的平行线交于点E.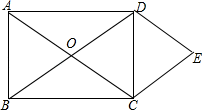 (1)、求证:四边形OCED为菱形;(2)、若AB=3,BC=4,求菱形OCED的面积.21. 为了推广阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图1和图2,请根据有关信息,解答下列问题:
(1)、求证:四边形OCED为菱形;(2)、若AB=3,BC=4,求菱形OCED的面积.21. 为了推广阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图1和图2,请根据有关信息,解答下列问题: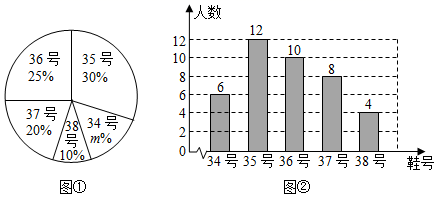 (1)、本次接受随机抽样调查的学生人数为 , 图1中m的值是;(2)、求本次调查获取的样本数据的众数和中位数;(3)、根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?22. 直线y=ax﹣1经过点(4,3),交y轴于点A.直线y=﹣0.5x+b交y轴于点B(0,1),且与直线y=ax﹣1相交于点C.(1)、求点C的坐标;(2)、求ABC的面积.23. 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,甲、乙两人间的距离为s(km)与甲行驶的时间为t(h)之间的关系如图所示.
(1)、本次接受随机抽样调查的学生人数为 , 图1中m的值是;(2)、求本次调查获取的样本数据的众数和中位数;(3)、根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?22. 直线y=ax﹣1经过点(4,3),交y轴于点A.直线y=﹣0.5x+b交y轴于点B(0,1),且与直线y=ax﹣1相交于点C.(1)、求点C的坐标;(2)、求ABC的面积.23. 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,甲、乙两人间的距离为s(km)与甲行驶的时间为t(h)之间的关系如图所示.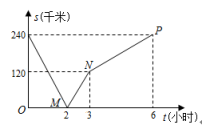 (1)、以下是点M、点N、点P所代表的实际意义,请将M、N、P填入对应的横线上.
(1)、以下是点M、点N、点P所代表的实际意义,请将M、N、P填入对应的横线上.①甲到达终点;
②甲乙两人相遇;
③乙到达终点;
(2)、AB两地之间的路程为千米;(3)、求甲、乙各自的速度.24. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将 沿AE对折至 ,延长交BC于点G,连接AG.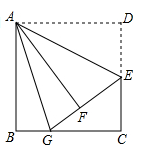 (1)、求证: ;(2)、求BG的长.25. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
(1)、求证: ;(2)、求BG的长.25. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)、若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?(2)、在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?26. 如图1,直线分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.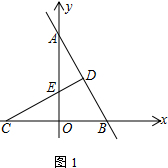
 (1)、点B的坐标为 , 不等式的解集为;(2)、若 , 求点D的坐标;(3)、如图2,以CD为边作菱形CDFG,且∠CDF=60°,连接AF、CF、AC,求证:CAF≌△CBD.
(1)、点B的坐标为 , 不等式的解集为;(2)、若 , 求点D的坐标;(3)、如图2,以CD为边作菱形CDFG,且∠CDF=60°,连接AF、CF、AC,求证:CAF≌△CBD.