吉林省白城市通榆县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中是二次根式的是（）

A、 $\sqrt{- 7}$ B、 $\sqrt{a}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt[3]{3}$

查看试题解析
2. 若 $y = k x - 4$ 的函数值y随x的增大而增大，则k的值可能是下列的（）

A、-4 B、 $- \frac{1}{2}$ C、0 D、3

查看试题解析
3. 下列各组数中，不能做为直角三角形的三边长的是（）

A、1.5，2，3 B、7，24，25 C、6，8，10 D、9，12，15

查看试题解析
4. ▱ABCD中，AC、BD是两条对角线，如果添加一个条件，可推出▱ABCD是菱形，那么这个条件可以是（　　）

A、AB=CD B、AC=BD C、AC⊥BD D、AB⊥BD

查看试题解析
5. 将四根长度相等的细木条首尾顺次相接，用钉子钉成四边形ABCD，转动这个四边形，使它的形状改变，当 $∠ B = 90 °$ ，如图①测得 $A C = 2 \sqrt{2}$ ，当 $∠ B = 60 °$ 时，如图②则AC的长度为（）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{6}$ D、 $2 \sqrt{2}$

查看试题解析
6. 若k≠0，b<0，则y＝kx+b的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 函数 $y = \sqrt{x - 3}$ 中，自变量x的取值范围是．

查看试题解析
8. 若函数y=（m﹣1）x^|m|是正比例函数，则该函数的图象经过第象限．

查看试题解析
9. 某市在一次空气污染指数抽查中，收集到10人的数据如下，61，75.81，56，81，91，92，91，75，81．该组数据的众数是．

查看试题解析
10. 将直线y＝2x向上平移3个单位所得的直线解析式是．

查看试题解析
11. 有两名学员小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是．

查看试题解析
12. 一个长为120m，宽为100m的矩形场地，要扩建为一个正方形场地，设长增加xm，宽增加ym，则y与x之间的函数关系式为．

查看试题解析
13. 如图，点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是．

查看试题解析
14. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB＝5，AD＝12，则四边形ABOM的周长为．

查看试题解析

三、解答题

15. 计算：3 $\sqrt{3}$ ﹣ $\sqrt{8}$ + $\sqrt{2}$ ﹣ $\sqrt{27}$ ．

查看试题解析
16. 先化简，再求值：当 $a = 9$ 时，求 $a + \sqrt{1 - 2 a + a^{2}}$ 的值．小宁的解答过程如下：
原式＝ $a + \sqrt{(1 - a)^{2}}$ 第一步
$= a + 1 - a$ 第二步
＝1 第三步

(1)、小宁的解答从第步出现错误的，错误的原因是．

(2)、写出正确的解答过程：

查看试题解析
17. 如图，一根树在离地面9米处撕裂，树的顶部落在离底部12米处，求折断之前树高多少米．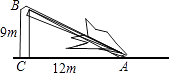

查看试题解析
18. 如图，菱形ABCD的对角线AC，BD相交于点O，且DE∥AC，AE∥BD．求证：四边形AODE是矩形．

查看试题解析
19. 如图是边长为1的小正方形网格，每个小正方形的顶点叫做格点，点A、C均在格点上，且AC＝5，请选择适当的格点，只用无刻度的直尺在网格中完成下列画图．

(1)、在图①中过点A画出线段AB，使AB＝AC（点B在格点上），并且AB在AC上方．

(2)、在（1）的条件下，请在图②中画出以AB为一边的平行四边形ABMN，满足 $S_{平行四边形 A B M N} = 2 S_{△ A B C}$ ．

查看试题解析
20. 平面直角坐标系xOy中，已知点A（0，3）、点B（3，0），一次函数y＝2x的图象与直线AB交于点M．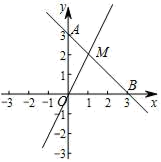

(1)、求直线AB的函数解析式及M点的坐标；

(2)、若点N是x轴上一点，且△MNB的面积为6，求点N的坐标．

查看试题解析
21. 如图，在 $△ A B C$ 中，∠ACB＝90°，AB＝20，AC＝12，把 $△ A B C$ 沿AD折叠，使AB落在直线AC上．

(1)、BC＝；

(2)、求重叠部分（阴影部分）的面积．

查看试题解析
22. 某中学为了解全校学生参加课外体育活动情况，随机抽取了n名学生，调查他们一周参加课外体育活动的时间（单位：h），并将所得数据绘制成如下的统计图表．
n名学生一周参加课外体育活动的时间频数分布表
时间段
频数
$0 < t \leq 2$
9
$2 < t \leq 4$
40
$4 < t \leq 6$
81
$6 < t \leq 8$
62
$8 < t \leq 10$
8

(1)、求n的值，并补全频数分布直方图；

(2)、这组数据的中位数落在频数分布表中的哪个时间段？

(3)、根据上述调查结果，估计该校1800名学生中一周参加课外体育活动时间在6h以上的人数．

查看试题解析
23. 如图，在▱ABCD中，对角线AC与BD交于点O．点E，F在BD上，且BE=DF．连接AE并延长，交BC于点G，连接CF并延长，交AD于点H．

(1)、求证：四边形AGCH是平行四边形；

(2)、若AC平分∠HAG，求证：四边形AGCH是菱形．

查看试题解析
24. 抗击新冠疫情期间，一方危急，八方支援：当我省疫情严重时，急需大量医疗防护物资，现知A城有医疗防护物资200t，B城有医疗防护物资300t，现要把这些医疗物资全部运往C、D两市．从A城往C、D两市的运费分别为20元/t和25元/t；从B城往C、D两市的运费分别为15元/t和24元/t，现C市需要物资240t，D市需要物资260t．请回答下列问题：
调入地
调出地
C
D
总计
A
x
200
B
300
总计
240
260
500

(1)、若设从A城往C市运xt完成下表（写化简后的式子）．

(2)、求调运物资总运费y与x之间的函数关系式，写出自变量取值范围．（运费＝调运物资的重量×每吨运费）

(3)、求出怎样调运物资可使总运费最少？最少运费是多少？

查看试题解析
25. 甲、地相距300km，一辆货车和一辆轿车先后从甲地匀速开往乙如图地，轿车晚出发1h．货车和轿车各自与甲地的距离y（单位：km）与货车行驶的时间x（单位：小时）之间的关系如图所示．

(1)、求出图中的m和n的值；

(2)、求出货车行驶过程中 $y_{2}$ 关于x的函数解析式，并写出自变量x的取值范围；

(3)、当轿车到达乙地时，求货车与乙地的距离．

查看试题解析
26. 如图，在等边 $△ A B C$ 中，AB＝24cm．射线 $A G ∥ B C$ ，点E从点A出发沿射线AG以 $3 c m / s$ 的速度运动．同时点F从点B出发沿射线BC以5cm/s的速度运动，设点E的运动时间为t（s）．解答下列问题：

(1)、点F在线段BC上运动时，CF＝cm；当点F在线段BC的延长线上运动时，CF＝cm（用含t的式子表示）．

(2)、在整个的运动过程中，当以A、C、E、F为顶点的四边形是平行四边形时，求t值；

(3)、在整个的运动过程中，是否存在某一时刻，使E、F两点间的距离最小，若存在，求出t值：若不存在，说明理由．

查看试题解析

时间段	频数
$0 < t \leq 2$	9
$2 < t \leq 4$	40
$4 < t \leq 6$	81
$6 < t \leq 8$	62
$8 < t \leq 10$	8

调入地调出地	C	D	总计
A	x		200
B			300
总计	240	260	500