黑龙江省哈尔滨市五常市2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{\frac{a}{5}}$ B、 $\sqrt{8}$ C、 $\sqrt{x^{2}}$ D、 $\sqrt{x^{2} + 1}$

查看试题解析
2. 要使式子 $\sqrt{1 - x}$ 有意义，则x的取值范围是（）

A、x≤1 B、x≥1 C、x＞0 D、x＞﹣1

查看试题解析
3. 若函数 $y = (k + 1) x + k^{2} - 1$ 是正比例函数，则 $k$ 的值为（）

A、1 B、0 C、 $± 1$ D、 $- 1$

查看试题解析
4. 一次函数 $y = 2 x - 3$ 的图像不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（）

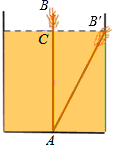A、15尺 B、16尺 C、17尺 D、18尺

查看试题解析
6. 某市测得一周PM2.5的日均值（单位：）如下：50，40，75，50，37，50，40，这组数据的中位数和众数分别是（）

A、50和50 B、50和40 C、40和50 D、40和40

查看试题解析
7. 一位工人师傅测量一个等腰三角形工件的腰，底及底边上的高，并按顺序记录下数据，量完后，不小心与其他记录的数据记混了，请你帮助这位师傅从下列数据中找出等腰三角形工件的数据（）

A、13，10，10 B、13，10，12 C、13，12，12 D、13，10，11

查看试题解析
8. 下列说法中，正确的是（）

A、有一个角是直角的平行四边形是正方形； B、对角线相等的四边形是平行四边形； C、四条边相等的四边形是菱形； D、矩形的对角线一定互相垂直．

查看试题解析
9. 如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的 $B^{'}$ 处，若AE＝2，DE＝6，∠EFB＝60°，则梯形ABFE的面积是（）

A、6 B、16 C、 $6 \sqrt{3}$ D、 $16 \sqrt{3}$

查看试题解析
10. 甲乙两队举行一年一度的端午节赛龙舟比赛，两队在比赛时的路程s（米）与时间t（分钟）之间的函数关系图象如图所示．下列说法：（1）乙队率先到达终点；（2）乙队比甲队少用了0.2分钟；（3）出发时甲队比乙队速度大；（4）两队在t＝3.4分钟时相遇．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算 $\sqrt{9 a} + \sqrt{25 a} =$ ．

查看试题解析
12. 某校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%、20%、30%的比例计入学期总评成绩，90分以上为优秀．甲、乙丙三人的各项成绩如下表（单位：分）

纸笔测试
实践能力
成长记录
甲
90
83
95
乙
98
90
95
丙
80
88
90
则学期总评成绩优秀的是．

查看试题解析
13. 现有甲、乙两个合唱队队员的平均身高为170cm，方差分别是 ${S_{甲}}^{2}$ 、 ${S_{乙}}^{2}$ ，且 ${S_{甲}}^{2} > {S_{乙}}^{2}$ ，则两个队的队员的身高较整齐的是．

查看试题解析
14. 若一个长方体的长为 $2 \sqrt{6} c m$ ，宽为 $\sqrt{3} c m$ ，高为 $\sqrt{2} c m$ ，则它的体积为
cm³ ．

查看试题解析
15. 若直角三角形的三边长分别是n+1，n+2，n+3，则n的值为．

查看试题解析
16. 如图，一次函数y＝kx＋b的图象如图所示，当y＜0时，x的取值范围是

查看试题解析
17. 把直线y＝－x＋3向上平移m个单位后，与直线y＝2x＋4的交点在第一象限，则m的取值范围是.

查看试题解析
18. 有一组数据如下：3，a，4，6，7，它们的平均数是5，那么这组数据的方差是．

查看试题解析
19. 已知，一次函数 $y = k x + b$ ，当 $2 \leq x \leq 5$ 时， $- 3 \leq y \leq 6$ ．则 $k + b$ 的值是．

查看试题解析
20.
如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE= $\frac{1}{3}$ CD，过点B作BF∥DE，与AE的延长线交于点F．若AB=6，则BF的长为

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{12} - \sqrt{3} + \sqrt{21} \times \sqrt{28}$

(2)、 $(2 \sqrt{48} - 3 \sqrt{27}) \div \sqrt{6}$

查看试题解析
22. 阅读下列材料：
小明遇到这样一个问题：已知：在△ABC中，AB，BC，AC三边的长分别为 $\sqrt{5}$ 、 $\sqrt{10}$ 、 $\sqrt{13}$ ，求△ABC的面积．

小明是这样解决问题的：如图1所示，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法．

请回答：

(1)、①图1中△ABC的面积为 ▲ ；
②图1中过O点画一条线段MN，使MN＝2AB，且M、N在格点上．

(2)、图2是一个6×6的正方形网格（每个小正方形的边长为1）．利用构图法在图2中画出三边长分别为 $\sqrt{37}$ 、2 $\sqrt{10}$ 、 $\sqrt{41}$ 的格点△DEF．

查看试题解析
23. 光华中学七年级举行跳绳比赛，要求每班选出5名学生参加，在规定时间每人跳绳不低于150次为优秀，冠、亚军在甲、乙两班中产生．下表是这两个班的5名学生的比赛数据（单位：）

1号
2号
3号
4号
5号
平均次数
方差
甲班
150
148
160
139
153
150
46.8
乙班
139
150
145
169
147
a
103.2
根据以上信息，解答下列问题：

(1)、写出表中a的值和甲、乙两班的优秀率；

(2)、写出两班比赛数据的中位数；

(3)、你认为冠军奖应发给那个班？简要说明理由．

查看试题解析
24.
如图，四边形ABCD为平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E．

(1)、求证：BE=CD；

(2)、连接BF，若BF⊥AE，∠BEA=60°，AB=4，求平行四边形ABCD的面积．

查看试题解析
25. “六一”前夕，某玩具经销商用去2350元购进A、B、C三种新型的电动玩具共50套，并且购进的三种玩具都不少于10套，设购进A种玩具x套，B种玩具y套，三种电动玩具的进价和售价如表所示
型号
A
B
C
进价（元/套）
40
55
50
售价（元/套）
50
80
65

(1)、求y与x之间的函数关系式；

(2)、假设所购进的这三种玩具能全部卖出，且在购销这种玩具的过程中需要另外支出各种费用200元．
①求出利润P（元）与x（套）之间的函数关系式；
②求出利润的最大值，并写出此时三种玩具各多少套．

查看试题解析
26. 如图1，在正方形ABCD中，E、F分别是BC、DC上的两点且EF＝BE＋DF．

(1)、求证：∠EAF＝45°

(2)、如图2，作∠EFC的平分线FG交AE的延长线于G，连接CG，求证： $B C - C F = \frac{\sqrt{2}}{2} C G$ ；

查看试题解析
27. 已知：如图，直线OB解析式为 $y = \sqrt{3} x$ ，点B的纵坐标为 $2 \sqrt{3}$ ，点A的坐标为 $(4 ， 0)$ ．

(1)、求直线AB的解析式：

(2)、动点P从原点O出发，以每秒1个单位的速度在线段OA上向终点A运动，过P作PC⊥x轴，交OB于C，过C作CD⊥y轴，交AB于D，设点P的运动时间为t秒，线段CD的长为d，求出d关于t之间的函数关系式，并直接写出自变量t的取值范围；

查看试题解析

	纸笔测试	实践能力	成长记录
甲	90	83	95
乙	98	90	95
丙	80	88	90

	1号	2号	3号	4号	5号	平均次数	方差
甲班	150	148	160	139	153	150	46.8
乙班	139	150	145	169	147	a	103.2

型号	A	B	C
进价（元/套）	40	55	50
售价（元/套）	50	80	65