北京市延庆区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列曲线中,表示y是x的函数的是 ( )A、
2. 下列曲线中,表示y是x的函数的是 ( )A、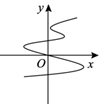 B、
B、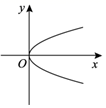 C、
C、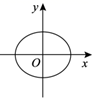 D、
D、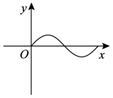 3. 在平面直角坐标系中,下列各点在第四象限的是( )A、 B、 C、 D、4. 下列各点中,在直线上的点是( )A、 B、 C、 D、5. 下列多边形中,内角和与外角和相等的是( )A、
3. 在平面直角坐标系中,下列各点在第四象限的是( )A、 B、 C、 D、4. 下列各点中,在直线上的点是( )A、 B、 C、 D、5. 下列多边形中,内角和与外角和相等的是( )A、 B、
B、 C、
C、 D、
D、 6. 下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩(单位:cm)的平均数与方差:
6. 下表记录了甲、乙、丙、丁四名跳高运动员最近10次训练成绩(单位:cm)的平均数与方差:甲
乙
丙
丁
平均数
181
183
183
181
方差
1.6
3.4
1.6
3.4
要选择一名成绩好且发挥稳定的同学参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁7. 矩形和菱形都一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线长度相等 D、对角线平分一组对角8. 某农业基地现有杂交水稻种植面积36公顷,计划两年后将杂交水稻种植面积增加到48公顷,设该农业基地杂交水稻种植面积的年平均增长率为x,则可列方程为( )A、 B、 C、 D、二、填空题
-
9. 函数y= 中,自变量x的取值范围是 .10. 方程的解为 .11. 如图,在平行四边形中, , , 的平分线交于点E,则的长为 .
 12. 如图,A,B两点被池塘隔开,在直线外选一点C,连接和分别取 , 的中点D,E,测得D,E两点间的距离为10 m,则A,B两点间的距离为m.
12. 如图,A,B两点被池塘隔开,在直线外选一点C,连接和分别取 , 的中点D,E,测得D,E两点间的距离为10 m,则A,B两点间的距离为m. 13. 请写出一个图形经过一、三象限的正比例函数的解析式 .14. 关于x 的一元二次方程有两个不相等的实数根,则m的取值范围是 .15. 如果点与点都在直线上,那么mn(填“>”、“<”或“=”).16. 平面直角坐标系中,直线与相交于点 , 下列结论中正确的是(填写序号).
13. 请写出一个图形经过一、三象限的正比例函数的解析式 .14. 关于x 的一元二次方程有两个不相等的实数根,则m的取值范围是 .15. 如果点与点都在直线上,那么mn(填“>”、“<”或“=”).16. 平面直角坐标系中,直线与相交于点 , 下列结论中正确的是(填写序号).
①关于x,y的方程组的解是;
②关于x的不等式的解集是;
③ .
三、解答题
-
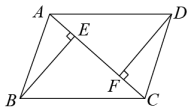
17. 解方程:(1)、;(2)、 .18. 如图,已知四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,求证:BE=DF.
 19. 阅读下面材料:
19. 阅读下面材料:在数学课上,老师提出如下问题:
已知:如图,在中, .
求作:矩形 .

小明的思考过程是:
①由于求作矩形,回顾了矩形的定义和判定:
矩形的定义:有一个角是直角的平行四边形叫做矩形;
矩形判定1:对角线相等的平行四边形是矩形;
矩形判定2:有三个角是直角的四边形是矩形.
②条件给出了 , 可以选矩形的定义或者矩形判定2;经过思考,小明选择了“矩形定义”.
③小明决定通过作线段AC的垂直平分线,作出线段的中点O,再倍长线段 , 从而确定点D的位置.
小明的作法如下:
作法:①分别以点A,C为圆心,大于的同样长为半径作弧,两弧分别交于点E,F;
③作直线 , 直线交于点O;
③作射线 , 在上截取 , 使得;
④连接 , .
∴ 四边形就是所求作的矩形.

请你根据小明同学设计的尺规作图过程:
(1)、使用直尺和圆规,依作法在图1中补全图形(保留作图痕迹);(2)、完成下面的证明:证明:∵直线是的垂直平分线,
∴ ,
∵ ,
∴四边形是平行四边形( ① )(填推理的依据).
∵ ,
∴四边形是矩形( ② )(填推理的依据).
(3)、参考小明的作图思路,另外设计一种作法,利用直尺和圆规在图2中完成.(温馨提示:保留作图痕迹,不用写作法和证明)
 20. 已知一次函数()的图像经过点和点 , 与y轴交于点C.
20. 已知一次函数()的图像经过点和点 , 与y轴交于点C. (1)、求这个一次函数的表达式;(2)、在坐标系中画出该一次函数的图象;(3)、求的面积.21. 已知关于x的一元二次方程 .(1)、如果该方程有两个相等的实数根,求m的值;(2)、如果该方程有一个根小于0,求m的取值范围.22. 如图,要在墙边围一个矩形花圃.花圃的一边靠墙(墙的长度不限),另三边用篱笆围成.如果矩形花圃的面积为50平方米,篱笆长20米,求矩形花圃的长和宽各是多少米?
(1)、求这个一次函数的表达式;(2)、在坐标系中画出该一次函数的图象;(3)、求的面积.21. 已知关于x的一元二次方程 .(1)、如果该方程有两个相等的实数根,求m的值;(2)、如果该方程有一个根小于0,求m的取值范围.22. 如图,要在墙边围一个矩形花圃.花圃的一边靠墙(墙的长度不限),另三边用篱笆围成.如果矩形花圃的面积为50平方米,篱笆长20米,求矩形花圃的长和宽各是多少米? 23. 某通信公司推出A,B,C三种上网收费方式,每月收取的费用 , , 与月上网时间x的对应关系如图所示.
23. 某通信公司推出A,B,C三种上网收费方式,每月收取的费用 , , 与月上网时间x的对应关系如图所示. (1)、对于上网方式A,若月上网时间在25小时以内,月收费为元;(2)、如果月上网时间超过35小时且不足55小时,选择方式最省钱?(3)、对于上网方式B,若月上网时间超过60小时,超出的时间每小时收费元;(4)、根据图象,写出一个其他的推断.24. 如图,在矩形中, , 相交于点O, , .
(1)、对于上网方式A,若月上网时间在25小时以内,月收费为元;(2)、如果月上网时间超过35小时且不足55小时,选择方式最省钱?(3)、对于上网方式B,若月上网时间超过60小时,超出的时间每小时收费元;(4)、根据图象,写出一个其他的推断.24. 如图,在矩形中, , 相交于点O, , .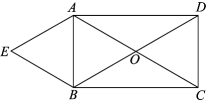 (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.25. 2022年2月20日晚,北京冬奥会圆满落幕.伴随着北京冬奥会的举行,全国各地掀起了参与冰雪运动、了解冬奥知识的热潮.为了调查同学们对冬奥知识的了解情况,某校进行了相关测试,获得了他们的成绩(单位:分),并随机抽取了50名学生的成绩,对数据(成绩)进行了整理、描述和分析.下面给出了相关信息:
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.25. 2022年2月20日晚,北京冬奥会圆满落幕.伴随着北京冬奥会的举行,全国各地掀起了参与冰雪运动、了解冬奥知识的热潮.为了调查同学们对冬奥知识的了解情况,某校进行了相关测试,获得了他们的成绩(单位:分),并随机抽取了50名学生的成绩,对数据(成绩)进行了整理、描述和分析.下面给出了相关信息:a.50名学生的测试分数(百分制)如下:
77 79 80 60 85 66 86 87 68 89
91 82 68 85 65 82 57 66 86 87
69 67 79 79 86 79 87 89 90 89
81 80 72 82 84 82 65 76 76 97
98 55 89 70 71 78 59 52 70 60
b.按如下分组整理、描述样本数据:
成绩x(单位:分)
频数
频率
4
0.08
a
0.20
12
b
20
0.40
4
0.08
合计
50
1.00

请根据以上信息,解答下列问题:
(1)、在频数分布表中, ,;(2)、补全频数分布直方图;(3)、该校有1000名学生,请你估计该校学生成绩不低于80分的人数.26. 在平面直角坐标系中,直线()与平行,且过点 , 过点A作y轴的垂线,垂足为点B.(1)、求k,b的值;(2)、点C在y轴上,点 , 四边形是矩形.①如果矩形的面积小于6,求m的取值范围;
②直线()与直线交于点E, , 直接写出点E的坐标.
27. 如图,四边形是正方形,点E是边上的点,连接 , , 过点D作 , 垂足为F,延长到点G,使 , 连接 , , 延长交的延长线于点H. (1)、依题意补全图形;(2)、用含α的式子表示;(3)、直接写出的度数;(4)、用等式表示线段 , , 之间的数量关系,并证明.28. 在平面直角坐标系中,对于直线l:()与图形M给出如下定义:若直线l与图形M有两个交点P,Q,则线段的长度称为直线l关于图形M的“截距”.如图,矩形的其中三个顶点的坐标为 , , .
(1)、依题意补全图形;(2)、用含α的式子表示;(3)、直接写出的度数;(4)、用等式表示线段 , , 之间的数量关系,并证明.28. 在平面直角坐标系中,对于直线l:()与图形M给出如下定义:若直线l与图形M有两个交点P,Q,则线段的长度称为直线l关于图形M的“截距”.如图,矩形的其中三个顶点的坐标为 , , .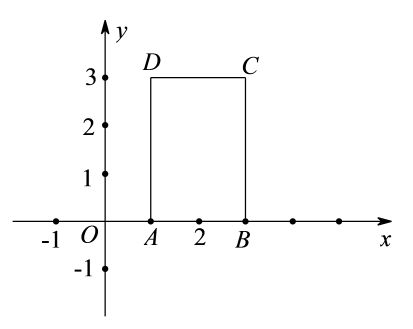 (1)、点C的坐标是 .(2)、直线关于矩形的“截距”是;
(1)、点C的坐标是 .(2)、直线关于矩形的“截距”是;直线关于矩形的“截距”是 , 求m的值.
(3)、如果直线()经过点 , 且关于矩形的“截距”的最小值是 , 求k的取值范围.