北京市平谷区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-25 类型:期末考试
一、单选题
-
1. 下列图形中,不是中心对称图形的是( )A、等边三角形 B、菱形 C、矩形 D、正方形2. 在平面直角坐标系中,点P(1,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 菱形具有而平行四边形不具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、四个角都相等4. 把一元二次方程配方后,下列变形正确的是( )A、 B、 C、 D、5. 下列多边形中,内角和为540°的是( )A、
 B、
B、 C、
C、 D、
D、 6. 在一次函数中,已知 , 那么在下面它的图像的示意图中,正确的是( )A、
6. 在一次函数中,已知 , 那么在下面它的图像的示意图中,正确的是( )A、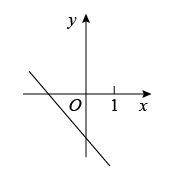 B、
B、 C、
C、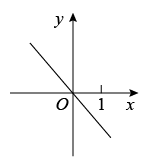 D、
D、 7. 已知一次函数 ,那么下列结论正确的是( )A、y 的值随 x 的值增大而增大 B、图象经过第一、二、三象限 C、图象必经过点 D、当 时,y<08. 北京市的一些公园分布示意图,图中分别以正东、正北方向为 x 轴、y 轴的正方向建立平面直角坐标系,有如下四个结论:
7. 已知一次函数 ,那么下列结论正确的是( )A、y 的值随 x 的值增大而增大 B、图象经过第一、二、三象限 C、图象必经过点 D、当 时,y<08. 北京市的一些公园分布示意图,图中分别以正东、正北方向为 x 轴、y 轴的正方向建立平面直角坐标系,有如下四个结论:①当表示什刹海公园的点的坐标为(0,0),表示日坛公园的点的坐标为(3,-2)时,表示北海公园的点的坐标为(0,-1);
②当表示地坛公园的点的坐标为(0,0),表示日坛公园的点的坐标为(4,-4)时,表示圆明园的点的坐标为(-8,7);
③当表示地坛公园的点的坐标为(1,1),表示北海公园的点的坐标为(0,0)时,表示什刹海公园的点的坐标为(0,1);
④当表示地坛公园的点的坐标为(1.5,1.5),表示日坛公园的点的坐标为(7.5,-4.5)时,表示圆明园的点的坐标为(-10.5,12).
上述结论中,所有符合题意结论的序号是( )
 A、①②③ B、②③④ C、①②④ D、①②③④
A、①②③ B、②③④ C、①②④ D、①②③④二、填空题
-
9. 在平面直角坐标系xOy中,直线与x轴交点坐标为 .10. 如图,在ABC中,D,E分别是AB,AC的中点,点F,G在边BC 上,且DFEG.只需添加一个条件即可证明四边形DFGE是矩形,这个条件可以是 . (写出一个即可)
 11. 如图,已知 , 那么的度数为
11. 如图,已知 , 那么的度数为 12. 在平面直角坐标系xOy中,如果点 A的坐标为(3,-4),那么线段OA长度为 .13. 农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种玉米的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到数据如图.
12. 在平面直角坐标系xOy中,如果点 A的坐标为(3,-4),那么线段OA长度为 .13. 农科院计划为某地选择合适的甜玉米种子.选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种玉米的相关情况,农科院各用10块自然条件相同的试验田进行试验,得到数据如图.
你认为应该选择哪种甜玉米种子 , 理由是 .
14. 在平面直角坐标系xOy中,将点B(-3,2)向右平移5个单位长度,再向下平移3个单位长度后与点A重合,则点A的坐标是 .15. 若关于x的一元二次方程有两个相等的实数根,则m的值是 .16. 如图,在矩形中, , M为的中点,沿过点M的直线翻折,使点C落在边上,记折痕为 , 则折痕的长为 .
三、解答题
-
17. 解方程:(1)、;(2)、18. 在平面直角坐标系xOy中,一次函数 的图象经过A(-2,0),B(1,3)两点.
 (1)、画出一次函数的图象;(2)、求这个一次函数的解析式;(3)、求OAB的面积.19. 如图,在平行四边形ABCD中,连接BD,取BD中点O,过点O作直线EF,分别交AD,BC于点E,F,求证:AE=CF.
(1)、画出一次函数的图象;(2)、求这个一次函数的解析式;(3)、求OAB的面积.19. 如图,在平行四边形ABCD中,连接BD,取BD中点O,过点O作直线EF,分别交AD,BC于点E,F,求证:AE=CF. 20. 在平面直角坐标系中,一次函数的图象是由函数的图象平移得到,且经过点 .(1)、求这个一次函数的解析式;(2)、当时,对于的每一个值,函数的值大于一次函数的值,直接写出的取值范围.21. 如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.
20. 在平面直角坐标系中,一次函数的图象是由函数的图象平移得到,且经过点 .(1)、求这个一次函数的解析式;(2)、当时,对于的每一个值,函数的值大于一次函数的值,直接写出的取值范围.21. 如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E. (1)、求证:四边形ACED是平行四边形;(2)、若AB= , DE=3,求BD的值.22. 十八世纪,古巴比伦泥板书上有这样一个问题:“一块矩形田地面积为55,长边比短边多6,问长边多长?”请用一元二次方程的知识解决这个问题.23. 已知关于x的一元二次方程x2−mx+m−2=0.(1)、求证:此方程总有两个不相等的实数根;(2)、若此方程有一个根是0,求出m的值和另一个根.24. 为了了解某中学八年级160名男生的身体发育情况,从中随机抽取了20名男生的身高进行测量,并对数据进行了整理、描述和分析,下面给出了部分信息.
(1)、求证:四边形ACED是平行四边形;(2)、若AB= , DE=3,求BD的值.22. 十八世纪,古巴比伦泥板书上有这样一个问题:“一块矩形田地面积为55,长边比短边多6,问长边多长?”请用一元二次方程的知识解决这个问题.23. 已知关于x的一元二次方程x2−mx+m−2=0.(1)、求证:此方程总有两个不相等的实数根;(2)、若此方程有一个根是0,求出m的值和另一个根.24. 为了了解某中学八年级160名男生的身体发育情况,从中随机抽取了20名男生的身高进行测量,并对数据进行了整理、描述和分析,下面给出了部分信息.a.20名男生身高数据如下(单位:cm):168 161 157 165 173 173 166 176 167 174 176 161 173 171 179 169 169 177 162 155
b.经分组整理后的频数分布表与频数分布直方图如图所示:
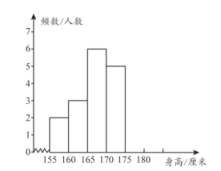
分组身高x厘米
频数
频率
155≤ x < 160
2
0.10
160≤ x < 165
3
b
165≤ x < 170
6
170≤ x < 175
0.25
175≤ x < 180
a
0.20
合计
20
1
但在列表和画图时,遗漏了频数分布表中的数据和频数分布直方图中相应的条形图.请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、样本数据中,男生身高的中位数是(4)、估计该校八年级男生身高在170-175cm范围内的人数约为25. 下面是小明设计的作正方形ABCD的尺规作图过程.
已知:RtABC中,∠ABC=90°,AB=CB
求作:正方形ABCD.
作法:如图,
①以点A为圆心,BC长为半径作弧;
②以点C为圆心,AB长为半径作弧;
③两弧交于点D.点B和点D在AC异侧;
④连接AD,CD.
所以四边形ABCD是正方形.
(1)、根据小明设计的尺规作图过程,使用直尺和圆规,补全图形(保留作图痕迹);(2)、完成下面的证明.证明:
∵AB= ▲ , BC= ▲ ,
∴四边形ABCD是平行四边形
∵∠ABC=90°,
∴四边形ABCD是矩形( )(填推理的依据),
又∵AB=BC,
∴四边形ABCD是正方形( )(填推理的依据).
26. “莓好生活,幸福家园”,春节期间,小明一家要去采摘草莓,现有甲、乙两家草莓采摘园草莓品质相同,销售价格也相同,且推出了如下的优惠方案:甲园:游客需购买门票,采摘的草莓六折优惠;
乙园:游客进园不需购买门票,采摘的草莓超过一定数量后,超过的部分打折优惠.
优惠期间,某游客的草莓采摘量为(千克),在甲园所需总费用为(元),在乙园所需总费用为(元), , 与之间的函数关系如图所示.
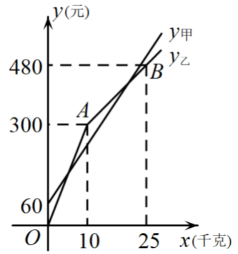 (1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克 元.(2)、求 与的函数表达式;(3)、当游客采摘千克草莓时,选择哪一家采摘园更便宜?
(1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克 元.(2)、求 与的函数表达式;(3)、当游客采摘千克草莓时,选择哪一家采摘园更便宜?
