安徽省黄山市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{2}{3}}$ C、 $\sqrt{2}$ D、 $\sqrt{x^{2}}$

查看试题解析
2. 下列计算错误的是（）

A、3+2 $\sqrt{2}$ =5 $\sqrt{2}$ B、 $\sqrt{8}$ ÷2= $\sqrt{2}$ C、 $\sqrt{2}$ × $\sqrt{3}$ = $\sqrt{6}$ D、 $\sqrt{8}$ $- \sqrt{2}$ = $\sqrt{2}$

查看试题解析
3. 要得到函数 $y = 3 x + 5$ 的图象，只需将函数 $y = 3 x$ 的图象（）

A、向左平移5个单位 B、向右平移5个单位 C、向下平移5个单位 D、向上平移5个单位

查看试题解析
4. 下列说法中，正确的有（）
⑴对角线相等且互相垂直的四边形是菱形
⑵有一个内角是60°的平行四边形是菱形
⑶对角线相等且互相垂直平分的四边形是正方形
⑷邻边相等的平行四边形是正方形
⑸顺次连接菱形各边中点所得的四边形是矩形

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若 $b > 0$ ，则一次函数 $y = x + b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在正方形网格中，每个小正方形边长都为1，则网格上△ABC中，边长为无理数的边长有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 已知 $\sqrt{x^{2} - 10 x + 25}$ ＝5﹣x，则x的取值范围是（）

A、为任意实数 B、0≤x≤5 C、x≥5 D、x≤5

查看试题解析
8. 第24届冬季奥林匹克运动会于2022年2月4日在北京隆重开幕，某社区举办了奥林匹克知识竞赛活动，此次竞赛共有10题，七名参赛者在此次竞赛活动中答对的题数分别为7、10、9、9、10、8、10．关于这组数据，下列结论中正确的是（）

A、方差是7 B、众数是9 C、平均数是8.5 D、中位数是9

查看试题解析
9.
如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD的面积的（　　）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{3}{10}$

查看试题解析
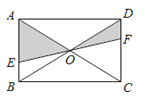10. 如图，矩形ABCD中，对角线AC，BD交于点O，E，F分别是边BC，AD的中点，AB＝2，BC＝4，一动点P从点B出发，沿着B﹣A﹣D﹣C在矩形的边上运动，运动到点C停止，点M为图1中某一定点，设点P运动的路程为x，△BPM的面积为y，表示y与x的函数关系的图象大致如图2所示．则点M的位置可能是图1中的（）

A、点C B、点O C、点E D、点F

查看试题解析

二、填空题

11. 函数 $y = \frac{\sqrt{x - 3}}{x + 5}$ 中，自变量x的取值范围是．

查看试题解析
12. 对于任意不相等的两个实数 $a$ 、 $b$ ，定义一种运算※如下： $a$ ※ $b$ $= \frac{\sqrt{a + b}}{a - b}$ ．如：4※3 $= \frac{\sqrt{4 + 3}}{4 - 3} = \sqrt{7}$ ，那么9※7 $=$ ．

查看试题解析
13. 某中学生数学学科课堂表现为92分、平时作业为92分、期末考试为86分，若这三项成绩按2：3：5的比例计入总评成绩，则该中学生数学学科总评成绩为分．

查看试题解析
14. 若一次函数 $y = (1 + m) x + m - 3$ 的图象经过第一、三、四象限，则实数m的取值范围．

查看试题解析
15. 菱形的边长为5，一条对角线长为8，则此菱形的面积是．

查看试题解析
16. 若方程组 ${\begin{array}{l} 2 x + y = b \\ x - y = a \end{array}$ 的解是 ${\begin{array}{l} x = - 1 \\ y = 3 \end{array}$ ，则直线y＝﹣2x+b与直线y＝x﹣a的交点坐标是.

查看试题解析
17. 在平面直角坐标系中，若点A、B的坐标分别为（0，2）和（n，n＋4），则线段AB长的最小值为．

查看试题解析
18. 如图，菱形ABCD的边长是4，∠A=60°，点G为AB的中点，以BG为边作菱形BEFG，其中点E在CB的延长线上，点P为FD的中点，连接PB．则PB= ．

查看试题解析

三、解答题

19. 计算： $| 1 - \sqrt{3} | - \sqrt{3} \times \sqrt{12} + \frac{1}{2 - \sqrt{3}} - {(\frac{2}{3})}^{- 1}$

查看试题解析
20. 先化简，再求值： $(\frac{1}{x + y} - \frac{2}{x^{2} + x y}) \div \frac{x - 2}{2 x}$ ，其中实数x、y满足 $y = \sqrt{x - 3} - \sqrt{6 - 2 x} + 1$ ．

查看试题解析
21. 如图，在由边长为1个单位长度的中小正方形组成的12×12的网格中，给出了以格点（网格线的交点）为端点的线段AB．

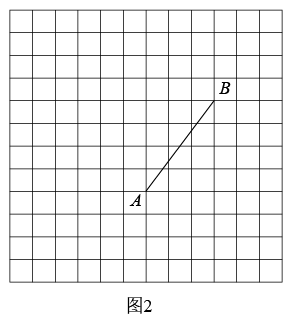(1)、在图1中以线段AB为一边，作一个菱形ABCD，且点C、D也为格点．（画出一个即可）

(2)、在图2中使用无刻度的直尺，作出线段AB的垂直平分线，并保留必要的作图痕迹．

查看试题解析
22. 某校要从小王和小李两名同学中挑选一人参加全市知识竞赛，在最近的五次选拔测试中他俩的成绩（单位：分）如表：
姓名
第1次
第2次
第3次
第4次
第5次
小王
60
75
100
90
75
小李
70
85
100
80
80

(1)、完成表格：
姓名
平均成绩
中位数
众数
方差
小王
80
75
75
190
小李

(2)、在这五次测试中，成绩比较稳定的同学是谁？若将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少？

(3)、历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为选谁参加比赛比较合适？请说明理由．

查看试题解析
23. 如图，已知矩形ABCD，AB=4，AD=6，点E是BC的中点，将△DCE沿DE折叠得到ΔDC₁E，连接BC₁、CC₁ ， CC₁与DE交于点G．求BC₁的长度．

查看试题解析
24. 某公司开发出一款新的节能产品，该产品的成本价为 $6$ 元 $/$ 件，该产品在正式投放市场前通过代销点进行了为期一个月 $(30$ 天 $)$ 的试营销，售价为 $8$ 元 $/$ 件，工作人员对销售情况进行了跟踪记录，并将记录情况绘成图象.图中的折线 $O D E$ 表示日销售量y(件)与销售时间x(天)之间的函数关系，已知线段 $D E$ 表示的函数关系中，时间每增加 $1$ 天，日销售量减少 $5$ 件.

(1)、第 $26$ 天的日销售量是件，日销售利润是元.

(2)、求y与x之间的函数关系式，并写出x的取值范围；

(3)、日销售利润不低于 $600$ 元的天数共有多少天？试销售期间，日销售最大利润是多少元？

查看试题解析

姓名	第1次	第2次	第3次	第4次	第5次
小王	60	75	100	90	75
小李	70	85	100	80	80

姓名	平均成绩	中位数	众数	方差
小王	80	75	75	190
小李