安徽省滁州市定远县张桥片2021-2022学年八年级下学期期末数学试题

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 函数 $y = \frac{\sqrt{x + 2}}{x^{2} - 9}$ 的自变量x的取值范围是（）

A、x≠±3 B、x≤﹣2 C、x≠3 D、x≥﹣2且x≠3

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ C、 $\sqrt{(- 2) \times (- 5)} = \sqrt{- 2} \times \sqrt{- 5}$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
3. 下列方程是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} = 1$ B、 $a x^{2} + b x + c = 0$ C、 $(x + 1) (x + 2) = 1$ D、 $(x - 3)^{2} + 4 = x^{2}$

查看试题解析
4. 下列命题①方程 $k x^{2} - x - 2 = 0$ 是一元二次方程；② $x = 1$ 与方程 $x^{2} = 1$ 是同解方程；③方程 $x^{2} = x$ 与方程 $x = 1$ 是同解方程；④由 $(x + 1) (x - 1) = 9$ 可得 $x + 1 = 3$ 或 $x - 1 = 3$ ，其中正确的命题有（）．

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 已知关于 $x$ 的一元二次方程 $(m - 1) x^{2} + x + 1 = 0$ 有实数根，则 $m$ 的取值范围是（）

A、 $m \leq \frac{5}{4}$ B、 $m < \frac{5}{4}$ 且 $m \neq 1$ C、 $m \geq \frac{5}{4}$ D、 $m \leq \frac{5}{4}$ 且 $m \neq 1$

查看试题解析
6. 如图， $△ A B C$ 和 $△ E C D$ 都是等腰直角三角形， $△ A B C$ 的顶点 $A$ 在 $△ E C D$ 的斜边 $D E$ 上 $.$ 下列结论：其中正确的有（）
① $△ A C E$ ≌ $△ B C D$ ；② $∠ D A B = ∠ A C E$ ；③ $A E + A C = A D$ ；④ $A E^{2} + A D^{2} = 2 A C^{2}$

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
7. 已知 $\frac{a^{2} - 9}{a + 3} = 0$ ，且 $\sqrt{b - 4} + (5 - c)^{2} = 0$ ，则以a、b、c为三边长的三角形为（）

A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
8. 如图，以正五边形ABCDE的边DE为边向外作等边三角形△DEF，连接AF，则∠AFE等于（）

A、6° B、8° C、12° D、14°

查看试题解析
9. 如图，在长方形ABCD中， $A B = 4$ ， $B C = 8$ ，对角线AC的垂直平分线分别交AD、AC于点M，N，连接CM，则CM的长为（）

A、 $2 \sqrt{5}$ B、 $- 2 \sqrt{5}$ C、 $- 5$ D、5

查看试题解析
10. 如图是交警在一个路口统计的某个时段来往车辆的车速（单位：千米/小时）情况，则下列关于车速描述错误的是（）

A、平均数是23 B、中位数是25 C、众数是30 D、方差是129

查看试题解析

二、填空题

11. 已知 $x y > 0$ ，化简二次根式 $x \sqrt{- \frac{y}{x^{2}}}$ 的正确结果是

查看试题解析
12. 为响应“把中国人的饭碗牢牢端在自己手中”的号召，确保粮食安全，优选品种，提高产量，某农业科技小组对原有的小麦品种进行改良种植研究．在保持去年种植面积不变的情况下，今年预计小麦平均亩产量将在去年的基础上增加a%，因为优化了品种，预计每千克售价将在去年的基础上上涨2a%，全部售出后预计总收入将增加68%，则a的值为．

查看试题解析
13. 如图， $△ A B C$ 与 $△ A D E$ 均是等腰直角三角形，点B，C，D在同一直线上， $A B = A C = 2$ ， $A D = A E = 3$ ， $∠ B A C = ∠ D A E = 90 °$ ，则CD= ．

查看试题解析
14. 如图，在▱ABCD中，点E在对角线AC上，AD＝AE＝BE，∠D＝102°，则∠BAE的大小是．

查看试题解析

三、解答题

15. 计算： $\sqrt{20} + \sqrt{5} \times \sqrt{\frac{4}{5}} + | 2 - \sqrt{5} |$ ．

查看试题解析
16. 解方程： $2 {(x - 2)}^{2} - 4 = 0$ ．

查看试题解析
17. 阅读下列解题过程：
$\frac{1}{\sqrt{2} + 1} = \frac{(\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{(\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
$\frac{1}{\sqrt{4} + \sqrt{3}} = \frac{(\sqrt{4} - \sqrt[]{3})}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})} = \sqrt{4} - \sqrt{3}$ ；……

(1)、 $\frac{1}{\sqrt{10} + \sqrt{9}} =$ ； $\frac{1}{\sqrt{100} + \sqrt{99}} =$ ．
观察上面的解题过程，请直接写出式子 $\frac{1}{\sqrt{n} + \sqrt{n - 1}} =$ ．

(2)、利用这一规律计算：
$(\frac{1}{\sqrt{2} + 1} + \frac{1}{(\sqrt{3} + \sqrt{2})} + \frac{1}{(\sqrt{4} + \sqrt{3})} + ⋯ + \frac{1}{(\sqrt{2021} + \sqrt{2020}}) \cdot (\sqrt{2021} + 1)$ 的值．

查看试题解析
18. 为庆祝中国共产党建党100周年，某区组织了学生参加党史知识竞赛，并从中抽取了200名学生的成绩（得分取正整数，满分为100分）进行统计，根据成绩分成如下5组：A.50.5～60.5，B.60.5～70.5，C.70.5～80.5，D.80.5～90.5，E.90.5～100.5．并绘制成两个统计图．

(1)、频数分布直方图中的a＝， b＝；

(2)、在扇形统计图中，D组所对应扇形的圆心角为n°，求n的值；

(3)、求E组共有多少人？该区共有1200名学生参加党史知识竞赛，如果设定获得一等奖的分数不低于91分，那么请你通过计算估计全区获得一等奖的人数是多少？

查看试题解析
19. 如图，沿AC方向开山修路．为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B取∠ABD＝120°，BD＝400米，∠D＝30°．那么另一边开挖点E离D多远正好使A、C、E三点在一直线上（ $\sqrt{3}$ ≈1.732，结果精确到1米）？

查看试题解析
20. 在 $△ A B C$ 中， $A B = A C = 5$ ．

(1)、如图①，若 $B C = 6$ ，点 $M 、 N$ 分别在 $B C 、 A C$ 上，将 $△ A B C$ 沿 $M N$ 折叠，使得点 $C$ 与点 $A$ 重合，求折痕 $M N$ 的长；

(2)、如图②，点 $D$ 在 $B C$ 延长线上，且 $B C ： C D = 2 ： 3$ ，若 $A D = 10$ ，求证： $△ A B D$ 是直角三角形．

查看试题解析
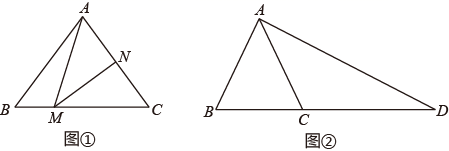21. 随着合肥都市圈的成立，合肥市将加大对都市圈内基础设施投人，尽快形成合肥都市圈“1小时通勤圈”和“1小时生活圈”．在都市圈内，计划四年完成对某条重要道路改造工程，2019年投入资金2000万元，2021年投入的资金为2420万元，设这两年问每年投人资金的年平均增长率相同．

(1)、求出这两年间的年平均增长率．

(2)、若对该道路投人资金的年平均增长率不变，预计完成这条道路改造工程的总投入．

查看试题解析
22. 如图，在 $▱ A B C D$ 中，对角线 $A C$ 的中点为O，点E为 $B C$ 上的动．点，连接 $E O$ ，并延长 $E O$ 交 $A D$ 于点F．

(1)、求证： $O E = O F$ ．

(2)、连接 $A E$ ， $C F$ ，若 $A C ⊥ E F$ ，试判断四边形 $A E C F$ 的形状，并给出证明过程．

查看试题解析
23. 如图，四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $A O = C O$ ， $E F$ 过点 $O$ 且与 $A D$ 、 $B C$ 分别相交于点 $E$ 、 $F$ ， $O E = O F$

(1)、求证：四边形 $A B C D$ 是平行四边形；

(2)、连接 $A F$ ，若 $E F ⊥ A C$ ， $Δ A B F$ 周长是15，求四边形 $A B C D$ 的周长.

查看试题解析