北京市房山区2021－2022学年高二下学期数学期末检测试卷

试卷更新日期：2022-08-25 类型：期末考试

进入出卷网下载

一、单选题

1. 已知函数 $f (x) = 2 x + 1$ ，则 $\underset{Δ x \to 0}{l i m} \frac{f (2 + Δ x) - f (2)}{Δ x}$ 的值为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 已知数列 ${a_{n}}$ 是等差数列， $a_{6} = 5 ， a_{3} + a_{8} = 15$ ，则 $a_{9}$ 的值为（）

A、15 B、-15 C、10 D、-10

查看试题解析
3. 商场举行抽奖活动，已知中奖率为 $\frac{1}{4}$ ，现有3位顾客抽奖，则恰有1位中奖的概率为（）

A、 $\frac{3}{64}$ B、 $\frac{9}{64}$ C、 $\frac{27}{64}$ D、 $\frac{3}{4}$

查看试题解析
4. 已知 $(2 x + 1)^{6} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4} + a_{5} x^{5} + a_{6} x^{6}$ ，则 $a_{1}$ 的值为（）

A、6 B、12 C、60 D、192

查看试题解析
5. 函数 $f (x) = x - l n x$ 的单调递减区间为（）

A、 $(- \infty ， 1]$ B、 $[1 ， + \infty)$ C、 $(0 ， 1]$ D、 $(0 ， + \infty)$

查看试题解析
6. 有一批同一型号的产品，已知其中由一厂生产的占30%，二厂生产的占70%．这两个厂的产品次品率分别为1%，2%，则从这批产品中任取一件，该产品是次品的概率是（）

A、0.015 B、0.03 C、0.0002 D、0.017

查看试题解析
7. 已知数列 ${a_{n}}$ 满足 $a_{2} > 0$ ，且对于任意正整数p，q都有 $a_{p} a_{q} = 2^{p + q}$ 成立，则 $a_{5}$ 的值为（）

A、8 B、16 C、32 D、64

查看试题解析
8. 已知无穷等差数列 ${a_{n}}$ 为递增数列， $S_{n}$ 为数列前n项和，则以下结论正确的是（）

A、 $S_{n + 1} > S_{n}$ B、数列 ${S_{n}}$ 有最大项 C、数列 ${n a_{n}}$ 为递增数列 D、存在正整数 $N_{0}$ ，当 $n > N_{0}$ 时， $a_{n} > 0$

查看试题解析
9. 已知函数 $f (x)$ 在 $[- π ， π]$ 上的图象如图所示，则函数 $f (x)$ 的解析式可能为（）

A、 $f (x) = e^{x} s i n x$ B、 $f (x) = e^{- x} s i n x$ C、 $f (x) = - e^{x} s i n x$ D、 $f (x) = - e^{- x} s i n x$

查看试题解析
10. 已知函数 $f (x) = e^{2} - 2 e^{| x |}$ ，以下4个命题：
①函数 $f (x)$ 为偶函数；②函数 $f (x)$ 在区间 $[1 ， e]$ 单调递减；③函数 $f (x)$ 存在两个零点；④函数 $f (x)$ 存在极大值和极小值．正确命题的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. $f (x) = s i n x$ ，则 $f^{'} (0) =$ ．

查看试题解析
12. 在由正数组成的等比数列 ${a_{n}}$ 中，若 $a_{4} a_{5} a_{6} = 1$ ，则 $a_{1} a_{2} a_{3} a_{4} a_{5} a_{6} a_{7} a_{8} a_{9}$ 的值为．

查看试题解析
13. 篮球运动员在比赛中每次罚球得分的规则是：命中得1分，不中得0分．已知某篮球运动员罚球命中的概率为0.9，设其罚球一次的得分为X，则X的方差 $D (X) =$ ．

查看试题解析
14. 一个口袋中装有7个球，其中有5个红球，2个白球抽到红球得2分，抽到白球得3分．现从中任意取出3个球，则取出3个球的得分Y的均值 $E (Y)$ 为．

查看试题解析
15. 数列 ${a_{n}}$ 为1，1，2，1，1，3，1，1，1，1，4，…，前n项和为 $S_{n}$ ，且数列 ${a_{n}}$ 的构造规律如下：首先给出 $a_{1} = 1$ ，接若复制前面为1的项，再添加1的后继数为2，于是 $a_{2} = 1 ， a_{3} = 2$ ，然后复制前面所有为1的项，1，1，再添加2的后继数为3，于是 $a_{4} = 1 ， a_{5} = 1 ， a_{6} = 3$ ，接下来再复制前面所有为1的项，1，1，1，1，再添加3的后继数为4，…，如此继续．现有下列判断：
① $a_{30} = 6$ ； ② $S_{30} = 40$ ；
③ $a_{1034} = 11$ ； ④ $S_{2022} = 2077$ ．
其中所有正确结论的序号为．

查看试题解析

三、解答题

16. 已知等差数列 ${a_{n}}$ 的前n项和为 $S_{n} ， a_{2} = 4 ， S_{4} = 20$ ，且 $b_{n} = 2^{a_{n}}$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、证明数列 ${b_{n}}$ 是等比数列；

(3)、求数列 ${a_{n} + b_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
17. 已知函数 $f (x) = - x^{3}$ 在 $x = 0$ 处的切线l．

(1)、求切线l的方程；

(2)、在同一坐标系下画出 $f (x) = - x^{3}$ 的图象，以及切线l的图象；

(3)、经过点 $(2 ， - 1)$ 做 $f (x) = - x^{3}$ 的切线，共有条．（填空只需写出答案）

查看试题解析
18. 某市统计部门随机调查了50户居民去年一年的月均用电量（单位： $k W \cdot h$ ），并将得到数据按如下方式分为6组： $[170 ， 190) ， [190 ， 210) ， ⋯ ， [270 ， 290)$ ，绘制得到如图的频率分布直方图：

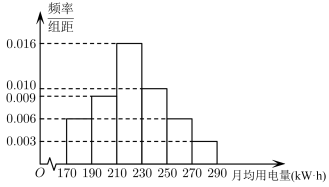(1)、从该市随机抽取一户，估计该户居民月均用电量在 $210 k W \cdot h$ 以下的概率；

(2)、从样本中月均用电量在 $[250 ， 290)$ 内的居民中抽取2户，记抽取到的2户月均用电量落在 $[270 ， 290)$ 内的个数为X，求X的分布列及数学期望．

查看试题解析
19. 已知 $f (x) = (x^{2} - 4 x + 1) e^{x}$ ．

(1)、求 $f (x)$ 的单调区间；

(2)、若在区间 $[- 4 ， 0]$ 上，函数 $f (x)$ 的图象与直线 $y = a$ 总有交点，求实数a的取值范围．

查看试题解析
20. 开展中小学生课后服务，是促进学生健康成长、帮助家长解决接送学生困难的重要举措，是进一步增强教育服务能力、使人民群众具有更多获得感和幸福感的民生工程某校为确保学生课后服务工作顺利开展，制定了两套工作方案，为了解学生对这两个方案的支持情况，对学生进行简单随机抽样，获得数据如下表：

男
女
支持方案一
24
16
支持方案二
25
35
假设用频率估计概率，且所有学生对活动方案是否支持相互独立．

(1)、从样本中抽1人，求已知抽到的学生支持方案二的条件下，该学生是女生的概率；

(2)、从该校支持方案一和支持方案二的学生中各随机抽取1人，设X为抽出两人中女生的个数，求X的分布列与数学期望；

(3)、在（2）中，Y表示抽出两人中男生的个数，试判断方差 $D (X)$ 与 $D (Y)$ 的大小．（直接写结果）

查看试题解析
21. 若数列 ${a_{n}}$ 中存在三项，按一定次序排列构成等比数列，则称 ${a_{n}}$ 为“ $Δ$ 数列”．

(1)、分别判断数列1，2，3，4，与数列2，6，8，12是否为“ $Δ$ 数列”，并说明理由；

(2)、已知数列 ${b_{n}}$ 的通项公式为 $b_{n} = 2^{n + 1} + 1$ ，判断 ${b_{n}}$ 是否为“ $Δ$ 数列”，并说明理由；

(3)、已知数列 ${c_{n}}$ 为等差数列，且 $c_{1} \neq 0 ， c_{n} \in Z (n \in N^{*})$ ，求证 ${c_{n}}$ 为“ $Δ$ 数列”．

查看试题解析

	男	女
支持方案一	24	16
支持方案二	25	35