重庆市万州区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 在方程 $\frac{1}{2} x = x + 1$ ， $2 x + 3 y = 5$ ， $2 y - 1 = x$ ， $x - y + z = 0$ 中二元一次方程的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知 $a > b$ ，则下列不等式不一定成立的是（）

A、 $a + c > b + c$ B、 $a - c > b - c$ C、 $a c^{2} > b c^{2}$ D、 $\frac{a}{c^{2} + 1} > \frac{b}{c^{2} + 1}$

查看试题解析
4. 若 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于x，y的二元一次方程 $3 x - 2 = 3 a - 4 y$ 的解，则常数a的值的为（）

A、 $\frac{3}{8}$ B、3 C、1 D、4

查看试题解析
5. 五边形的内角和是（）

A、180° B、360° C、540° D、720°

查看试题解析
6. 下列关于平移的叙述不正确的是（）

A、一个图形经过平移后图形的形状不变 B、一个三角形经过平移后三角形的周长不变 C、一个三角形经过平移后三角形的面积不变 D、一个三角形平移前后对应点的连线互相平行

查看试题解析
7. 一个等腰三角形的三边长分别为3cm、acm、6cm，则它的周长是（）

A、12cm B、15cm C、12cm或15cm D、不能确定

查看试题解析
8. 我国古代数学名著《孙子算经》记载一道题：“一百马，一百瓦，大马一个拖三个，小马三个拖一个”，大意为：100匹马拉100片瓦，已知1个大马拖3片瓦，3匹小马拖一片瓦，问有多少匹大马，多少匹小马？若设有m匹大马，n匹小马，那么可列方程组为（）

A、 ${\begin{array}{l} m + n = 100 \\ 3 m + 3 n = 100 \end{array}$ B、 ${\begin{array}{l} m + n = 100 \\ 3 m + n = 100 \end{array}$ C、 ${\begin{array}{l} m + n = 100 \\ \frac{1}{3} m + n = 100 \end{array}$ D、 ${\begin{array}{l} m + n = 100 \\ 3 m + \frac{1}{3} n = 100 \end{array}$

查看试题解析
9. 定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x，下列式子中错误的是（　　）

A、[x]=x（x为整数） B、0≤x﹣[x]＜1 C、[x+y]≤[x]+[y] D、[n+x]=n+[x]（n为整数）

查看试题解析
10. 如图， $△ A B C ≌ △ C E D$ ，点D在BC边上， $∠ A + ∠ E = 90 °$ ， EC、ED与AB交于点F、G，则下列结论不正确的是（）

A、 $A C = C D$ B、 $∠ A C B = 90 °$ C、 $A B ⊥ C E$ D、 $E G = B G$

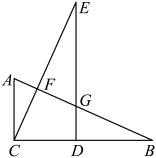查看试题解析
11. 某商场为促销对顾客实行优惠，规定：
（1）如一次性购物不超过200元，则不予优惠；
（2）如一次性购物超过200元，但不超过500元的，按标价给予9折优惠；
（3）如一次性购物超过500元的，其中500元按（2）给予优惠，超过500元的部分则给予8折优惠．
某人两次购物，分别付款160元与360元，如果他一次性购买这些商品，则应付（）

A、468元 B、498元 C、504元 D、520元

查看试题解析
12. 使得关于 $x$ 的不等式组 ${\begin{array}{l} - \frac{x}{2} \leq - \frac{m}{2} + 1 \\ - 2 x + 1 \geq 4 m - 1 \end{array}$ 有解，且使得关于 $y$ 的方程 $1 + (m - y) = 2 (y - 2)$ 有非负整数解的所有的整数 $m$ 的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

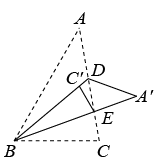
13. 已知有理数x、y满足 $| x - 3 | + {(2 y + 4)}^{2} = 0$ ，则代数式 $x + y$ 的值为．

查看试题解析
14. 用正六边形的瓷砖铺满地面，围绕一点拼在一起的正六边形瓷砖的块数是块．

查看试题解析
15. 如图， $△ A B C$ 中， $∠ A = 40 °$ ， D、E是AC边上的点，把 $△ A B D$ 沿BD对折得到 $△ A^{'} B D$ ，再把 $△ B C E$ 沿BE对折得到 $△ B C^{'} E$ ，若 $C^{'}$ 恰好落在BD上，且此时 $∠ C^{'} E B = 80 °$ ，则 $∠ A B C =$ ．

查看试题解析
16. 某食品加工厂在端午节期间制作红枣粽、腊肉粽、咸蛋粽进行销售，去年端午节期间销售的这三种粽子的数量之比为2∶3∶1，今年端午节期间销售这三种粽子不光保持了去年的销量，而且都还有所增加，其中腊肉粽增加的销量占今年总增加销量的 $\frac{2}{5}$ ．今年腊肉粽销售的数量占三种粽子销售总数量的 $\frac{8}{17}$ ，而红枣粽销售的总数量是咸蛋粽销售的总数量的2倍，则去年咸蛋粽销售的数量与今年咸蛋粽销售的数量之比为．

查看试题解析

三、解答题

17. 解下列方程（组）．

(1)、 $\frac{x}{2} - \frac{x - 1}{3} = 1$

(2)、 ${\begin{array}{l} 2 x + 3 y = 13 ① \\ x - y = - 1 ② \end{array}$

查看试题解析
18. 解不等式 $x - 3 (x - 2) > 2 (2 x - 3)$ ，然后把解集在数轴上表示出来，并写出最大整数解x的值．

查看试题解析
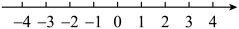19. 如图，在正方形网格中每个小正方形的边长都为1，每个正方形的顶点称为格点， $△ A B C$ 的三个顶点A、B、C均在格点上．

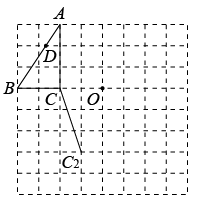(1)、请在网格上作出 $△ A B C$ 关于点O成中心对称的 $△ A_{1} B_{1} C_{1}$ ， A、B、C的对应点分别为 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ （不写作法）；

(2)、把 $△ A B C$ 沿着 $C C_{2}$ 方向平移得到 $△ A_{2} B_{2} C_{2}$ ，使A、B、C的对应点分别为 $A_{2}$ 、 $B_{2}$ 、 $C_{2}$ ，请在网格上作出 $△ A_{2} B_{2} C_{2}$ （不写作法）；

(3)、如图，D为AB上一点，根据所作的图形，直接写出 $△ D A_{2} B_{2}$ 的面积为．

查看试题解析
20. 对a、b、c、d规定一个运算法则为： $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ （等号右边是普通的减法运算）．

(1)、计算： $| \begin{array}{l} 1 & 2 \\ 3 & 4 \end{array} | =$ ， $| \begin{array}{l} 2 & m - n \\ - 4 & 2 m + n \end{array} | =$ ；

(2)、求出满足等式 $| \begin{array}{l} x - 2 & x \\ - 1 & \frac{1}{6} \end{array} | = | \begin{array}{l} 1 & 1 - x \\ \frac{1}{2} & 1 \end{array} |$ 的x的值．

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ B = 80 °$ ， $∠ C = 40 °$ ， $A D ⊥ B C$ 于D，点E为BC边上一点，连接AE．把 $△ A B E$ 沿着AE对折后，点B的对应点刚好落在AC边上的点F处．

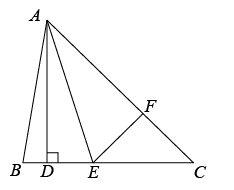(1)、求∠FEC的度数；

(2)、求∠DAE的度数．

查看试题解析
22. 为鼓励学生参加体育锻炼，学校体育组准备购买一批篮球和排球．已知篮球的单价比排球的单价多15元/个，买2个排球和3个篮球一共需要220元．

(1)、篮球和排球的单价分别是多少元？

(2)、体育组购买的篮球和排球总数量是36个，其中篮球的数量比排球的2倍还多，购买总资金不超过1700元，有几种购买方案？

查看试题解析
23. 把20根长度相等的木条分成三部分，分别用其中两部分木条首尾相连做成两个边数相等的多边形，再用剩下的一部分木条首尾相连做成一个多边形．

(1)、求这三个多边形的内角和；

(2)、如果前两个多边形的边数和大于后一个多边形的边数，求这三个多边形的边数．

查看试题解析
24. 在解决“已知有理数x、y、z满足方程组 ${\begin{array}{l} 2 x + 3 y - z = 5 ① \\ x - 2 y + 3 z = 1 ② \end{array}$ ，求 $4 x + 13 y - 9 z$ 的值”时，小华是这样分析与解答的．
解：由① $\times a$ 得： $2 a x + 3 a y - a z = 5 a$ ③，由② $\times b$ 得： $b x - 2 b y + 3 b z = b$ ④．
③＋④得： $(2 a + b) x + (3 a - 2 b) y + (- a + 3 b) z = 5 a + b$ ⑤．
当 $(2 a + b) x + (3 a - 2 b) y + (- a + 3 b) z = 4 x + 13 y - 9 z$ 时，
即 ${\begin{array}{l} 2 a + b = 4 \\ 3 a - 2 b = 13 \\ - a + 3 b = - 9 \end{array}$ ，解得 ${\begin{array}{l} a = 3 \\ b = - 2 \end{array}$ ．
∴① $\times 3 +$ ② $\times (- 2)$ ，得 $4 x + 13 y - 9 z = 5 \times 3 + 1 \times (- 2) = 13$ ．
请你根据小华的分析过程，解决如下问题：

(1)、若有理数a、b满足 $(3 x + 4 y + 2 z) \times a + (x + 6 y + 5 z) \times b = 12 x + 2 y - 5 z$ ，求a、b的值；

(2)、母亲节将至，小新准备给妈妈购买一束组合鲜花，若购买2枝红花、3枝黄花、1枝粉花共需18元；购买3枝红花、5枝黄花、2枝粉花共需28元．则购买1枝红花、3枝黄花、2枝粉花共需多少元？

查看试题解析
25. 已知 $M N ∥ P Q$ ，点A在MN上方，点D在PQ下方，分别以A、D为顶点作 $∠ A = ∠ D = 90 °$ ， $∠ A$ 的两边交MN于B、C（点B在点C的左边）， $∠ D$ 的两边交PQ于E、F（点E在点F的左边），AB、DE交于点G，AC、DF交于点H．

(1)、如图1，若 $∠ A B C = 45 °$ ， $∠ D F E = 30 °$ ，则 $∠ G =$ ， $∠ H =$ ；

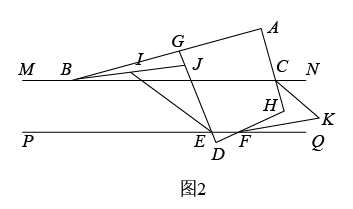
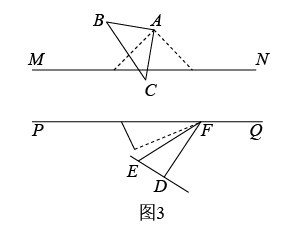(2)、如图2， $∠ A B C$ 、 $∠ P E G$ 的角平分线交于点I，BI交DG与J， $∠ N C H$ 、 $∠ Q F H$ 的角平分线交于点交K．试探索 $∠ J I E$ 、 $∠ K$ 之间的数量关系并说明理由；

(3)、在（1）的条件下，把 $△ A B C$ 绕点A顺时针方向旋转，每秒钟转3°，与此同时 $△ D E F$ 绕点F逆时针方向旋转，每秒钟转2°．当 $△ A B C$ 旋转到BC边首次与MN平行时，两个三角形都停止转动．在转动过程中，设旋转时间为t秒，当DE所在的直线与 $△ A B C$ 的边平行时，请直接写出t的所有可能的值．

查看试题解析