四川省自贡市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列调查中，最适合采用全面调查方式的是（）

A、调查某品牌洗衣机的使用寿命 B、调查自贡市五一期间进出主城区的车流量 C、调查某批次烟花爆竹的燃放效果 D、调查自贡市某校七年级一班学生的睡眠时间

查看试题解析
2. 如图，数轴上表示实数 $\sqrt{10}$ 的点可能是（）

A、点 $M$ B、点 $N$ C、点 $P$ D、点 $Q$

查看试题解析
3. 在平面直角坐标系中，点M（2，3）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 关于y的方程ay－2＝4与方程y－1＝1的解相同，则a的值是（）

A、2 B、3 C、4 D、－2

查看试题解析
5. 不等式5x＋1≤3x－1的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，将三角板的直角顶点放在两条平行线a，b中的直线b上，如果∠1＝42°，则∠2的度数是（）

A、30° B、40° C、48° D、45°

查看试题解析
7. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重.问：每只雀、燕的重量各为多少?设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A、 ${\begin{cases} 5 x + 6 y = 1 \\ 5 x - y = 6 y - x \end{cases}$ B、 ${\begin{cases} 6 x + 5 y = 1 \\ 5 x + y = 6 y + x \end{cases}$ C、 ${\begin{cases} 5 x + 6 y = 1 \\ 4 x + y = 5 y + x \end{cases}$ D、 ${\begin{cases} 6 x + 5 y = 1 \\ 4 x - y = 5 y - x \end{cases}$

查看试题解析
8. 对有理数x，y定义运算：x※y＝ax＋by，其中a，b是常数．若2※（－1）＝－6，2※3>2，则a，b的取值范围是（）

A、a>－2，b<2 B、a<－1，b<2 C、a<－1，b>2 D、a>－2，b>2

查看试题解析

二、填空题

9. 实数﹣3的相反数是　．

查看试题解析
10. 如果点P（m，1﹣2m）在第二象限，则m的取值范围是.

查看试题解析
11. 某校学生全部来自甲、乙、丙三个地区，其人数比为 $4 ： 3 ： 5$ ，若用扇形图表示上述分布情况，则“来自甲地区的学生”对应扇形的圆心角的度数为．

查看试题解析
12. 不等式组 ${\begin{array}{l} 2 x + 3 > 0 \\ 3 - x > 0 \end{array}$ 的整数解之和为．

查看试题解析
13. 如图，已知 $A B // D E ，$ ∠ABC=80°，∠CDE=140°，则∠BCD=.

查看试题解析
14. 将一副直角三角板如图放置，则下列结论：①∠1＝∠3；②如果∠2＝45°，则有BC $/ /$ AE；③如果∠2＝30°，则有DE $/ /$ AB；④如果∠2＝45°，必有∠4＝∠E．其中正确的有（填序号）．

查看试题解析

三、解答题

15. 计算： $| - 5 | - \sqrt[3]{- 8} + {(- 1)}^{2021}$ ．

查看试题解析
16. 解不等式 $\frac{x - 2}{5} - \frac{x + 4}{2} > - 3$ ，并把它的解集在数轴上表示出来．

查看试题解析
17. 解方程组
${\begin{array}{l} x + 5 y = 1 ① \\ x + 2 y = 7 ② \end{array}$

查看试题解析
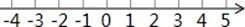18. 如图，方格纸中每个小正方形的边长为1cm，点A，B，C均为格点．

(1)、根据要求画图：
①过C点画直线 $M N ∥ A B$ ；
②将三角形ABC平移，使点A与点 $A^{'}$ 重合；

(2)、三角形ABC的面积＝ $c m^{2}$ ．

查看试题解析
19. 填空完成推理过程：
如图，∠1＝∠2，求证：∠B＝∠BCD．

证明：∵∠1＝  ▲   ，

∠1＝∠2（已知）．

∴∠2＝  ▲   ．（   ）．

∴ $A B ∥ C D$ （   ）．

∴∠B＝∠BCD（   ．

查看试题解析
20. 某校为积极响应巩固“全国文明城市”品牌建设，在每周五下午第三节课开展了丰富多彩的走班选课活动，其中综合实践类共开设了“礼行”“礼知”“礼思”“礼艺”“礼源”等五门课程，要求全校学生必须参与其中一门课程．为了解学生参与综合实践类课程活动情况，随机抽取了部分学生进行调查，根据调查结果绘制了如图所示不完整的条形统计图和扇形统计图．

(1)、请问被随机抽取的学生共有多少名？并补全条形统计图；

(2)、在扇形统计图中，求选择“礼行”课程的学生人数所对应的扇形圆心角的度数．

查看试题解析
21. 已知关于x，y的二元一次方程组 ${\begin{array}{l} x + 2 y = 3 \\ 3 x + 5 y = 2 m + 1 \end{array}$ 的解满足x＋y＝0，求实数m的值．

查看试题解析
22. 如图，已知AB∥CD，AD和BC交于点O，E为OC上一点，F为CD上一点，且∠CEF+∠BOD＝180°．说明∠EFC＝∠A的理由．

查看试题解析
23. 某市教育局对某镇实施“教育精准扶贫”，为某镇建了中、小两种图书馆.若建立 $3$ 个中型图书馆和 $5$ 个小型图书馆需要 $30$ 万元，建立 $2$ 个中型图书馆和 $3$ 个小型图书馆需要 $19$ 万元.

(1)、建立一个中型图书馆和一个小型图书馆各需要多少万元？

(2)、现要建立中型图书馆和小型图书馆共 $10$ 个，小型图书馆的数量不多于中型图书馆的数量，且总费用不超过 $45$ 万元，请问有几种方案？哪种方案所需费用最少？

查看试题解析
24. 如图1，在平面直角坐标系中，已知A（a，0），B（b，3），C（2，0），且满足 ${(a + b)}^{2} + \sqrt{a - b + 6} = 0$ ，线段AB交y轴于点F．

(1)、填空：a＝， b＝；

(2)、如图1，在x轴上是否存在点P，使得△ABP的面积与△ABC的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由；

(3)、如图2，点D为y轴正半轴上一点， $E D ∥ A B$ ，且AM，DM分别平分∠CAB，∠ODE，AM交y轴于点P，求∠AMD度数．

查看试题解析