四川省内江市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $a < b$ ，下列不等式不一定成立的是（）

A、 $a - 2 < b - 2$ B、 $- 2 a > - 2 b$ C、 $\frac{a}{2} < \frac{b}{2}$ D、 $a c^{2} > b c^{2}$

查看试题解析
2. 方程 $2 x - 3 y = 7$ ，用含y的代数式表示x为（）

A、 $x = \frac{1}{2} (7 - 3 y)$ B、 $x = \frac{1}{2} (7 + 3 y)$ C、 $y = \frac{1}{3} (7 - 2 x)$ D、 $y = \frac{1}{3} (2 - 7 x)$

查看试题解析
3. 习近平主席在2022年新年贺词中提到“人不负青山，青山定不负人”，一语道出“人与自然和谐共生”的至简大道．下列有关环保的四个图形中，是轴对称图形，但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如果x＝1是关于x的方程3x+4m﹣7＝0的解，则m的值是（）

A、1 B、﹣1 C、6 D、﹣6

查看试题解析
5. 已知多边形的每一个内角都等于150°，则这个多边形的边数是（）

A、9 B、10 C、11 D、12

查看试题解析
6. 用加减法解方程组 ${\begin{array}{l} 2 x - 3 y = 5 ① \\ 2 x - 8 y = 3 ② \end{array}$ 时， ①－②得（）

A、5y＝2 B、－11y＝8 C、－11y＝2 D、5y＝8

查看试题解析
7. 如图，将三角形 $A B C$ 沿 $B C$ 方向平移 $3 c m$ 得到三角形 $D E F$ ，若四边形 $A B F D$ 的周长为 $20 c m$ ，则三角形 $A B C$ 的周长是（）

A、 $17 c m$ B、 $14 c m$ C、 $11 c m$ D、 $8 c m$

查看试题解析
8. 下列说法正确的是（）

A、两个面积相等的图形一定是全等图形 B、两个全等图形形状一定相同 C、两个周长相等的图形一定是全等图形 D、两个正三角形一定是全等图形

查看试题解析
9. 用边长相等的两种正多边形进行密铺，其中一种是正八边形，则另一种正多边形可以是（）

A、正三角形 B、正方形 C、正五边形 D、正六边形

查看试题解析
10. 将无限循环小数 $0 . \overset{•}{7}$ 化为分数，可以设 $0 . \overset{•}{7}$ = $x$ ，则 $10 x = 7 + x$ ，解得： $x = \frac{7}{9}$ . 仿此，将无限循环小数 $0 . \overset{•}{2} \overset{•}{1}$ 化为分数为（）

A、 $\frac{7}{11}$ B、 $\frac{7}{33}$ C、 $\frac{21}{101}$ D、 $\frac{20}{99}$

查看试题解析
11. 若不等式组 ${\begin{array}{l} 2 x - 1 \geq 3 \\ x ＜ a \end{array}$ 的整数解共有三个，则a的取值范围是（）

A、4＜a＜5 B、4≤a＜5 C、4＜a≤5 D、4≤a≤5

查看试题解析
12. 如图，AB⊥AF，∠B、∠C、∠D、∠E、∠F的关系为（）

A、∠B+∠C+∠D+∠E+∠F＝270° B、∠B+∠C﹣∠D+∠E+∠F＝270° C、∠B+∠C+∠D+∠E+∠F＝360° D、∠B+∠C﹣∠D+∠E+∠F＝360°

查看试题解析

二、填空题

13. 若 $3 x - 5$ 的值为非负数，则x应满足．

查看试题解析
14. 如图，正方形 $A M N P$ 的边 $A M$ 在正五边形 $A B C D E$ 的边 $A B$ 上，则 $∠ P A E =$ $°$ ．

查看试题解析
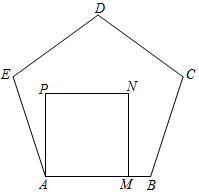15. 如果一个等腰三角形的两边长分别是5和7，则这个三角形的周长是.

查看试题解析
16. 若实数x，y满足方程组 ${\begin{array}{l} x - y = - 4 ， \\ x + y = 2 ， \end{array}$ 则 $(2 x + y)^{2022} =$ ．

查看试题解析

三、解答题

17. 解下列方程或不等式组：

(1)、 $x - 2 (5 - x) = 3 (2 x - 1)$ ；

(2)、解不等式组： ${\begin{array}{l} 3 (2 - x) \leq 2 x + 5 \\ \frac{4 x + 2}{3} < 1 + \frac{x}{6} \end{array}$ ．

查看试题解析
18. 如图，在方格纸中，每个小正方形的边长为1个单位长度， $△$ ABC的顶点都在格点上．

(1)、画出 $△$ ABC先向右平移4格，再向上平移1格得到的 $△$ A₁B₁C₁ ，其中点A，B，C的对应点分别为A₁ ， B₁ ， C₁；

(2)、画出 $△$ ABC关于点B₁成中心对称的图形A₂B₂C₂ ，其中点A，B，C的对应点分别为A₂ ， B₂ ， C₂；

(3)、连结C₁A₂ ， A₁A₂ ，求四边形A₁B₁C₁A₂的面积．

查看试题解析
19. 如图，在△ABC中，AD为边BC上的高，点E为边BC上的一点，连接AE.

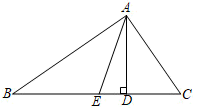(1)、当AE为边BC上的中线时，若AD=6，△ABC的面积为24，求CE的长；

(2)、当AE为∠BAC的角平分线时，若∠C=66°，∠B=36°，求∠DAE的度数.

查看试题解析
20. 已知关于 $x 、 y$ 的方程组 ${\begin{array}{l} x + y = a + 3 \\ x - y = 3 a - 1 \end{array}$ 的解是一对正数，求：

(1)、 $a$ 的取值范围；

(2)、化简： $| 2 a + 1 | - | a - 2 | .$

查看试题解析

21. 一方有难八方支援，某市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）

车型	甲	乙	丙
汽车运载量（吨/辆）	$5$	$8$	$10$
汽车运费（元/辆）	$400$	$500$	$600$

(1)、若全部物资都用甲、乙两种车型来运送，需运费

8200

元，问分别需甲、乙两种车型各几辆？

(2)、为了节约运费，该市政府可以调用甲、乙、丙三种车型参与运送，已知他们的总辆数为

16

辆，你能通过列方程组的方法分别求出几种车型的辆数吗？

(3)、求出哪种方案的运费最省？最省是多少元？

查看试题解析

22. 当光线经过镜面反射时，入射光线、反射光线与镜面所夹的角对应相等．例如：在图①，有 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ．设镜子 $A B$ 与 $B C$ 的夹角 $∠ A B C = α$ ．

(1)、如图①，若 $α = 90 °$ ，判断入射光线 $F E$ 与反射光线 $G H$ 的位置关系，并说明理由；

(2)、如图②，若 $α = 135 °$ ，设镜子 $C D$ 与 $B C$ 的夹角 $∠ B C D = θ$ （ $90 ° < θ < 180 °$ ），入射光线 $F E$ 与镜面 $A B$ 的夹角 $∠ 1 = β$ （ $0 ° < β < 90 °$ ），已知入射光线 $F E$ 分别从镜面 $A B$ 、 $B C$ 、 $C D$ 反射，反射光线 $H K$ 与入射光线 $F E$ 平行，请求出 $θ$ 与 $β$ 的关系式．

查看试题解析