四川省南充市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-24 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、±2 B、2 C、 D、2. 如图,科考队探测到目标位于图中阴影区域内,则目标的坐标可能是( )
 A、 B、 C、 D、3. 如图,直线AB,CD相交于点O, , OF平分 , 则的大小为( )
A、 B、 C、 D、3. 如图,直线AB,CD相交于点O, , OF平分 , 则的大小为( ) A、40° B、50° C、65° D、70°4. 某校为了了解全校2000名学生的视力情况,从中随机抽取了200名学生进行视力调查.在这个问题中,下列说法正确的是( )A、本次调查是全面调查 B、总体是2000名学生的视力情况 C、个体是200名学生的视力情况 D、样本容量是20005. 中国古代数学著作《孙子算经》中有一段文字大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱文:如果乙得到甲所有钱的 , 那么乙共有钱文,甲、乙两人原来各有多少钱?设甲、乙两人原来各有钱文,文,可列方程组为( )A、 B、 C、 D、6. 已知(其中),则下列不等式不一定成立的是( )A、 B、 C、 D、7. 关于x,y的二元一次方程组的解是 . 其中y的值被遮盖了,则m,y的值为( )A、 B、 C、 D、8. 如图,在三角形ABC中,点D,E,F分别在AB,AC,BC上, , , 则下列结论错误的是( )
A、40° B、50° C、65° D、70°4. 某校为了了解全校2000名学生的视力情况,从中随机抽取了200名学生进行视力调查.在这个问题中,下列说法正确的是( )A、本次调查是全面调查 B、总体是2000名学生的视力情况 C、个体是200名学生的视力情况 D、样本容量是20005. 中国古代数学著作《孙子算经》中有一段文字大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱文:如果乙得到甲所有钱的 , 那么乙共有钱文,甲、乙两人原来各有多少钱?设甲、乙两人原来各有钱文,文,可列方程组为( )A、 B、 C、 D、6. 已知(其中),则下列不等式不一定成立的是( )A、 B、 C、 D、7. 关于x,y的二元一次方程组的解是 . 其中y的值被遮盖了,则m,y的值为( )A、 B、 C、 D、8. 如图,在三角形ABC中,点D,E,F分别在AB,AC,BC上, , , 则下列结论错误的是( )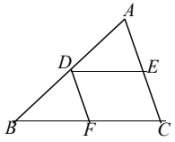 A、 B、 C、 D、9. 某班人去科技馆参观,科技馆票价是每人10元,但若购团体票(不低于50张),则可享受八五折优惠.班长算了算,购买50张票反而更合算,则m至少为( )A、42 B、43 C、44 D、4510. 如图,第二象限有两点 , 将线段AB平移,使点A,B分别落在两条坐标轴上,则平移后点B的对应点的坐标是( )
A、 B、 C、 D、9. 某班人去科技馆参观,科技馆票价是每人10元,但若购团体票(不低于50张),则可享受八五折优惠.班长算了算,购买50张票反而更合算,则m至少为( )A、42 B、43 C、44 D、4510. 如图,第二象限有两点 , 将线段AB平移,使点A,B分别落在两条坐标轴上,则平移后点B的对应点的坐标是( )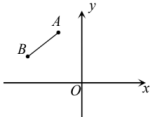 A、或 B、或 C、或 D、或
A、或 B、或 C、或 D、或二、填空题
-
11. 若 , 则的值是 .12. 如图,已知直线a∥b,∠1=60°,则∠2的度数是°.
 13. 经调查,某班同学上学所用的交通方式有:A.步行;B.骑自行车;C.乘公交车;D.其它;并根据调查结果绘制出扇形统计图(如图),则D所对应扇形的圆心角度数为度.
13. 经调查,某班同学上学所用的交通方式有:A.步行;B.骑自行车;C.乘公交车;D.其它;并根据调查结果绘制出扇形统计图(如图),则D所对应扇形的圆心角度数为度.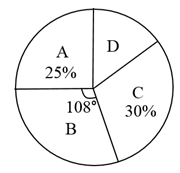 14. 某校教学楼在校门的正北200m处,实验楼在教学楼正西100m处,若实验楼的坐标为 , 则校门的坐标为 .15. 若关于x,y的二元一次方程组的解x,y互为相反数,则m的值为 .16. 我们知道 , 那么的整数部分就是 . 如果为的整数部分,且关于的不等式只有个负整数解,则实数的取值范围是 .
14. 某校教学楼在校门的正北200m处,实验楼在教学楼正西100m处,若实验楼的坐标为 , 则校门的坐标为 .15. 若关于x,y的二元一次方程组的解x,y互为相反数,则m的值为 .16. 我们知道 , 那么的整数部分就是 . 如果为的整数部分,且关于的不等式只有个负整数解,则实数的取值范围是 .三、解答题
-
17. 计算:18. 解不等式组: , 并写出它的整数解.19. 为了解“双减”落实情况,某初中学校随机调查了部分学生每天书面作业平均完成时间,并将调查结果绘制成不完整的频数分布表和频数分布直方图(如图),根据图表信息解答下列问题:
每天书面作业平均完成时间/h
频数
百分比
合计
 (1)、 , .(2)、补全频数分布直方图.(3)、教育部规定初中生每天书面作业完成时间平均不超过 , 该校共有名学生,试估计该校学生每天书面作业平均完成时间超出规定的人数.20. 如图,三角形AOB中,A,B两点的坐标分别为 , 将三角形AOB向左平移5个单位长度,再向上平移1个单位长度得到三角形 .
(1)、 , .(2)、补全频数分布直方图.(3)、教育部规定初中生每天书面作业完成时间平均不超过 , 该校共有名学生,试估计该校学生每天书面作业平均完成时间超出规定的人数.20. 如图,三角形AOB中,A,B两点的坐标分别为 , 将三角形AOB向左平移5个单位长度,再向上平移1个单位长度得到三角形 . (1)、在图中画出三角形 , 并分别写出点 , , 的坐标.(2)、求三角形AOB的面积.21. 打折前,买50件A商品和20件B商品用了1300元,买30件A商品和10件B商品用了750元.打折后,买100件A商品和100件B商品用了2800元,问比不打折少花了多少钱?22. 如图, , 于 , . 求证: .
(1)、在图中画出三角形 , 并分别写出点 , , 的坐标.(2)、求三角形AOB的面积.21. 打折前,买50件A商品和20件B商品用了1300元,买30件A商品和10件B商品用了750元.打折后,买100件A商品和100件B商品用了2800元,问比不打折少花了多少钱?22. 如图, , 于 , . 求证: . 23. 某景区的门票每张8元,一次性使用,考虑到人们的不同需求,也为了吸引更多的游客,该景区除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法,年票分A,B,C三类:A类年票每张100元,持票者进入景区时,无需再购买门票;B类年票每张50元,持票者进入该景区时,需再购买门票,每次2元;C类年票每张20元,持票者进入该景区时,需再购买门票,每次3元.(1)、如果只能选择一种购买门票的方式,并且计划在一年中花费80元在该景区的门票上,通过计算,找出可进入该景区次数最多的方式.(2)、一年中进入该景区不少于多少次时,购买A类年票比较合算?24. 阅读下列方程组的解法,然后解答相关问题:
23. 某景区的门票每张8元,一次性使用,考虑到人们的不同需求,也为了吸引更多的游客,该景区除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法,年票分A,B,C三类:A类年票每张100元,持票者进入景区时,无需再购买门票;B类年票每张50元,持票者进入该景区时,需再购买门票,每次2元;C类年票每张20元,持票者进入该景区时,需再购买门票,每次3元.(1)、如果只能选择一种购买门票的方式,并且计划在一年中花费80元在该景区的门票上,通过计算,找出可进入该景区次数最多的方式.(2)、一年中进入该景区不少于多少次时,购买A类年票比较合算?24. 阅读下列方程组的解法,然后解答相关问题:解方程组时,若直接利用消元法解,那么运算比较繁杂,采用下列解法则轻而易举
解:①-②,得 , 即 . ③
②-③×24,得 .
把代入③,解得 . 故原方程组的解是 .
(1)、请利用上述方法解方程组 .(2)、猜想并写出关于x,y的方程组的解,并加以检验.25. 如图,在直角坐标系中,点 , 分别在轴,轴上,且 . 轴,轴, , 交于点 , 为的中点. (1)、求点的坐标.(2)、点是线段上一点(不与点 , 重合),用含的式子表示并求整点(横、纵坐标均为整数)的坐标.(3)、点在上(点不与 , 重合), , 交于点 , , 的平分线交于点 . 当点P在线段上运动时,的大小是否变化?若不变,求出的度数;若变化,说明理由.
(1)、求点的坐标.(2)、点是线段上一点(不与点 , 重合),用含的式子表示并求整点(横、纵坐标均为整数)的坐标.(3)、点在上(点不与 , 重合), , 交于点 , , 的平分线交于点 . 当点P在线段上运动时,的大小是否变化?若不变,求出的度数;若变化,说明理由.