江苏省扬州市仪征市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 墨迹覆盖了等式“ $x^{3}$ $x = x^{2}$ （ $x \neq 0$ ）”中的运算符号，则覆盖的是（）

A、＋ B、－ C、× D、÷

查看试题解析
2. 下列各组长度的三条线段能组成三角形的是（）

A、1，2，3 B、1，1，2 C、2，2，3 D、1，3，7

查看试题解析
3. 若 $a < b$ ，则下列变形正确的是（）

A、 $a - 1 > b - 1$ B、 $\frac{a}{4} > \frac{b}{4}$ C、 $- 3 a > - 3 b$ D、 $1 - 2 a < 1 - 2 b$

查看试题解析
4. 一个多边形的内角和的度数可能是（）

A、1700° B、1800° C、1900° D、2000°

查看试题解析
5. 已知 $x = 1$ 是不等式 $2 x - b < 0$ 的解，b的值可以是（）

A、3 B、2 C、0 D、－2

查看试题解析
6. 如图，用不同的代数式表示图中阴影部分的面积，可得等式（）

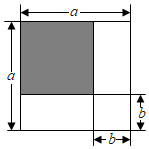A、（a＋b）²＝a²＋2ab＋b² B、（a﹣b）²＝a²＋2ab﹣b² C、（a＋b）（a﹣b）＝a²﹣b² D、（a﹣b）²＝a²﹣2ab＋b²

查看试题解析
7. 下列命题中，真命题是（）

A、相等的角是对顶角 B、不相交的两条直线是平行线 C、等角的余角相等 D、两条直线被第三条直线所截，同位角相等

查看试题解析
8. 如图，已知直线AB、CD被直线AC所截， $A B$ // $C D$ ， E是平面内任意一点（点E不在直线AB、CD、AC上），设 $∠ B A E = α$ ， $∠ D C E = β$ ．下列各式：① $α + β$ ， ② $α - β$ ， ③ $β - α$ ， ④ $180 ° - α - β$ ， $∠ A E C$ 的度数可能是（）

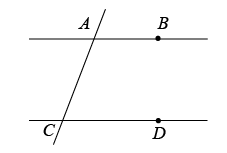A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题

9. 预防新型冠状病毒感染要用肥皂勤洗手，已知肥皂泡的厚度约为0.0000007m，将数据0.0000007用科学记数法表示为．

查看试题解析
10. 命题：“若m=n，则 $m^{2} = n^{2}$ ”的逆命题为.

查看试题解析
11. 若x²﹣ax+16是一个完全平方式，则a＝.

查看试题解析
12. ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ 是二元一次方程2x+ay＝5的一个解，则a的值为．

查看试题解析
13. 若 $3^{m} = 2$ ， $9^{n} = 10$ ，则 $3^{m + 2 n} =$ ．

查看试题解析
14. 计算： $202 2^{2} - 2024 \times 2020 =$ ．

查看试题解析
15. 如果不等式组 ${\begin{array}{l} x \geq 4 \\ x < m \end{array}$ 有解，那么m的取值范围是．

查看试题解析
16. 如图1，一个容量为600cm³的杯子中装有300cm³的水，将四颗相同的玻璃球放入这个杯子中，结果水没有满，如图2，设每颗玻璃球的体积为xcm³ ，根据题意可列不等式为．

查看试题解析
17. 如图，七边形ABCDEFG中，AB、ED的延长线交于点O．若与∠1、∠2、∠3、∠4相邻的四个外角的和等于230°，则∠BOD的度数为度．

查看试题解析
18. 如图，在△ABC中，依次取AB的中点 $D_{1}$ 、AC的中点 $D_{2}$ 、 $A D_{1}$ 的中点 $D_{3}$ 、 $A D_{2}$ 的中点 $D_{4}$ 、…，并连接 $C D_{1}$ 、 $D_{1} D_{2}$ 、 $D_{2} D_{3}$ 、 $D_{3} D_{4}$ 、……若△ABC的面积是1，则 $△ A D_{2021} D_{2022}$ 的面积是．

查看试题解析

三、解答题

19. 计算：

(1)、 ${(2022 - 3.14)}^{0} + 3^{2} - {(- \frac{1}{2})}^{- 2}$ ；

(2)、 $x \cdot (- x^{3}) + x^{6} \div x^{2}$ ．

查看试题解析
20. 分解因式：

(1)、 $a^{3} - a b^{2}$

(2)、 $3 x^{2} - 6 x y + 3 y^{2}$

查看试题解析
21. 先化简，再求值： $(x + 3) (x - 1) + (x - 2) (x + 2) - 2 {(x - 1)}^{2}$ ，其中 $x = \frac{1}{3}$ ．

查看试题解析
22. 解不等式组： ${\begin{array}{l} - 3 x + 5 \leq 2 \\ \frac{1}{2} (x + 1) < \frac{1}{3} x + 1 \end{array}$ ，并将解集在数轴上表示出来.

查看试题解析
23. 在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC向右平移3格，再向下平移2格，得到△DEF，使点A的对应点为点D，点B的对应点为点E，点C的对应点为点F．

(1)、画出△DEF；

(2)、在图中画出△ABC的AB边上的高线CG（保留利用格点的作图痕迹）；

(3)、△ABC的面积为；

(4)、若AB的长为5，AB边上的高 $C G =$ ．

查看试题解析
24. 如图， $∠ 1 = ∠ B C E$ ， $∠ 2 + ∠ 3 = 180 °$ ．

(1)、判断 $A C$ 与 $E F$ 的位置关系，并说明理由；

(2)、若 $C A$ 平分 $∠ B C E$ ， $E F ⊥ A B$ 于 $F$ ， $∠ 1 = 72 °$ ，求 $∠ B A D$ 的度数．

查看试题解析
25. 已知实数x、y满足2x+3y=1．

(1)、用含有x的代数式表示y；

(2)、若实数y满足y＞1，求x的取值范围；

(3)、若实数x、y满足x＞﹣1，y≥﹣ $\frac{1}{2}$ ，且2x﹣3y=k，求k的取值范围．

查看试题解析
26. 古运河是扬州的母亲河，为打造古运河风光带，现有一段长为180米的河道整治任务由A、B两个工程队先后接力完成．A工程队每天整治12米，B工程队每天整治8米，共用时20天．
根据题意，甲、乙两个同学分别列出了尚不完整的方程组如下：

甲： ${\begin{array}{l} x + y = □ \\ 12 x + 8 y = □ \end{array}$ 乙： ${\begin{array}{l} x + y = □ ① \\ \frac{x}{12} + \frac{y}{8} = □ ② \end{array}$

(1)、根据甲同学所列的方程组，请你指出未知数x、y表示的意义
甲：x表示， y表示；

请你补全乙同学所列的方程组：

乙：① ， ②；

(2)、求A、B两工程队分别整治河道多少米？（写出完整的解答过程）

查看试题解析
27. 阅读感悟：有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的一个代数式的值．如以下问题：已知实数x、y满足 $3 x - y = 5$ ， $2 x + 3 y = 7$ ，求 $x - 4 y$ 和 $7 x + 5 y$ 的值．本题常规思路是将 $3 x - y = 5$ ①， $2 x + 3 y = 7$ ②联立组成方程组，解得 $x$ 、 $y$ 的值再代入欲求值的代数式得到答案．常规思路计算量比较大，其实本题还可以仔细观察两个方程未知数系数之间的关系，通过适当变形整体求得代数式的值，如由①－②可得 $x - 4 y = - 2$ ，由①＋②×2可得 $7 x + 5 y = 19$ ．这样的解题思想就是通常所说的“整体思想”．
解决问题：

(1)、已知二元一次方程组 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = 5 \end{array}$ ，则 $x - y =$ ， $x + y =$ ；

(2)、试说明在关于x、y的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - 5 y = 3 a \end{array}$ 中，不论a取什么实数， $x + y$ 的值始终不变；

(3)、某班级组织活动购买小奖品，买3支铅笔、5块橡皮、1本笔记本共需21元，买4支铅笔、7块橡皮、1本笔记本共需28元，则购买10支铅笔、10块橡皮、10本笔记本共需多少元？

查看试题解析
28. 如图1，已知直线 $M N$ // $P Q$ ，直线GH分别与MN、PQ交于点H、G， $∠ 1 = 140 °$ ，一块直角三角板ABC，其中 $∠ C A B = 30 °$ ， $∠ C = 90 °$ ，它的斜边AB落在直线GH上，且点A与点G重合．

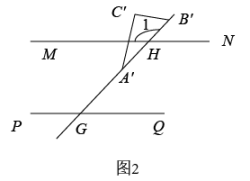
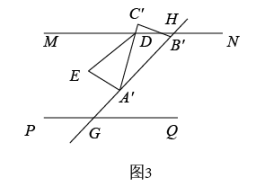(1)、求 $∠ C A Q$ 的度数；

(2)、将三角板沿着射线GH方向平移，平移后的三角形 $A^{'} B^{'} C^{'}$ ．
①如图2，当点 $C^{'}$ 落在 $∠ 1$ 的角平分线上时，求 $∠ A^{'} C^{'} H$ 的度数；
②如图3，当边 $A^{'} C^{'}$ 与直线MN相交于点D，分别作 $∠ M D A^{'}$ 与 $∠ D A^{'} G$ 的角平分线DE、 $A^{'} E$ 相交于点E，求 $∠ E$ 的度数；
③请你直接写出当 $△ A^{'} C^{'} H$ 为直角三角形时，求 $∠ N H C^{'}$ 的度数．

查看试题解析