江苏省扬州市广陵区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 北京2022年冬奥会会徽如图（一）是以汉字“冬”为灵感来源设计的．在下面的四个图中，能由图（二）经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 若x＞y，则（）

A、2x＜2y B、x＞y＋1 C、-3x＜-3y D、x-1＜y-1

查看试题解析
3. 下列各式中，正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{3} \cdot a^{3} = a^{9}$ C、 ${(a b)}^{2} = a^{2} b^{2}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
4. 已知 $a b = - 3$ ， $a + b = 2$ ，则 $a^{2} b + a b^{2}$ 的值是（）

A、6 B、﹣6 C、1 D、﹣1

查看试题解析
5. ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ 是下列哪个方程的一个解（）

A、3x＋y＝6 B、－2x＋y＝－3 C、6x＋y＝8 D、－x＋y＝1

查看试题解析
6. 下列选项中，可以用来说明命题“若 $| x | > 2$ ，则 $x > 2$ ”是假命题的反例是（）

A、 $x = - 3$ B、 $x = - 2$ C、 $x = 3$ D、 $x = 2$

查看试题解析
7. 如图，为了估计一池塘岸边两点A，B之间的距离，小丽同学在池塘一侧选取了一点P，测得PA＝5m，PB＝4m，那么点A与点B之间的距离不可能是（）

A、6.5m B、7.5m C、8.5m D、9.5m

查看试题解析
8. 为迎接2022年北京冬奥会，某校开展了以迎冬奥为主题的演讲活动，计划拿出180 元钱全部用于购买甲、乙两种奖品（两种奖品都购买），奖励表现突出的学生，已知甲种奖品每件15元，乙种奖品每件10元，则购买方案有（）

A、5种 B、6种 C、7种 D、8种

查看试题解析

二、填空题

9. 冠状病毒是一类病毒的总称，其最大直径约为0.00000012米，数据0.00000012科学记数法表示为．

查看试题解析
10. 命题“如果a+b=0，那么a，b互为相反数”的逆命题为.

查看试题解析
11. 二元一次方程x﹣3y＝8写成用含y的代数式表示x的形式为．

查看试题解析
12. 已知关于 $x$ 的不等式组 ${\begin{array}{l} x > a \\ x > b \end{array}$ ，其中 $a ， b$ 在数轴上的对应点如图所示，则这个不等式组的解集为.

查看试题解析
13. 已知 $a^{m} = 3$ ， $a^{n} = 2$ ，则 $a^{2 m - n}$ 的值为．

查看试题解析
14. 如果实数 $x$ ， $y$ 满足方程组 ${\begin{array}{l} x - 2 y = - 7 \\ x + y = 6 \end{array}$ ，那么 $(2 x - y)^{2022} =$ ．

查看试题解析
15. 求值： $202 2^{2022} \times (\frac{1}{2022})^{2021} =$ ．

查看试题解析
16. 一次数学测试，满分为100分.测试分数出来后，同桌的李华和吴珊同学把他俩的分数进行计算，李华说：我俩分数的和是160分，吴珊说：我俩分数的差是60分.那么，对于下列两个命题：①俩人的说法都是正确的；②至少有一人说错了；③俩人的说法都是错的.其中真命题是.（用序号填写）

查看试题解析
17. 已知关于 $x$ 的不等式 $2 x - m < 1 - x$ 的正整数解是1，2，3，则 $m$ 的取值范围是．

查看试题解析
18. 如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F=33°，则∠E= ．

查看试题解析

三、解答题

19. 计算：

(1)、 $(3 - π)^{0} + {(- \frac{1}{3})}^{- 3} + {(- 3)}^{3} \div {(- 3)}^{2}$ ；

(2)、 $(x - 2)^{2} - (x - 1) (x + 3)$ .

查看试题解析
20. 因式分解：

(1)、 $x^{2} y - 9 y$ ；

(2)、 $2 x^{3} - 8 x^{2} y + 8 x y^{2}$ ．

查看试题解析
21. 解方程组：

(1)、 ${\begin{array}{l} 6 x - 5 y = 3 \\ 6 x + y = - 15 \end{array}$

(2)、 ${\begin{array}{l} x + 4 y = 14 \\ \frac{x - 3}{4} - \frac{y - 3}{3} = \frac{1}{12} \end{array}$

查看试题解析
22. 解不等式组： ${\begin{array}{l} 5 x + 12 \geq 2 \\ \frac{2 x - 1}{3} < 1 \end{array}$ ，把解集表示在数轴上，并写出所有非负整数解．

查看试题解析
23. 如图是由若干个边长为1个单位长度的小正方形组成的方格图，三角形ABC在该方格图中．

(1)、将三角形ABC向左平移4个单位长度，得到三角形A₁B₁C₁（点A₁与点A对应，点B₁与点B对应，点C₁与点C对应），请在方格图中画出三角形A₁B₁C₁；

(2)、请求出三角形A₁B₁C₁的面积．

查看试题解析
24. 已知：如图，CD⊥AB，FG⊥AB，垂足分别为D，G，点E在AC上，且∠1=∠2，那么DE与BC平行吗？为什么？

查看试题解析
25. 如图，若AE是△ABC边上的高，∠EAC的角平分线AD交BC于D，∠ACB=40°，求∠ADE.

查看试题解析
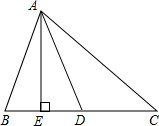26. 探究问题：已知 $∠ A B C$ ，画一个角 $∠ D E F$ ，使 $D E / / A B ， E F / / B C$ ，且 $D E$ 交 $B C$ 于点 $P$ . $∠ A B C$ 与 $∠ D E F$ 有怎样的数量关系？

(1)、我们发现 $∠ A B C$ 与 $∠ D E F$ 有两种位置关系：如图1与图2所示.
①图1中 $∠ A B C$ 与 $∠ D E F$ 数量关系为；图2中 $∠ A B C$ 与 $∠ D E F$ 数量关系为.请选择其中一种情况说明理由.

②由①得出一个真命题（用文字叙述）：.

(2)、应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数.

查看试题解析
27. 接种新冠病毒疫苗，建立全民免疫屏障，是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心，据调查得知，2辆 $A$ 型冷链运输车与3辆 $B$ 型冷链运输车一次可以运输600盒：5辆 $A$ 型冷链运输车与6辆 $B$ 型冷链运输车一次可以运输1350盒.

(1)、求每辆 $A$ 型车和每辆 $B$ 型车一次可以分别运输多少盒疫苗.

(2)、计划用两种冷链运输车共12辆运输这批疫苗， $A$ 型车一次需费用5000元， $B$ 型车一次需费用3000元.若运输物资不少于1500盒，且总费用小于54000元.请你列出所有运输方案，并指出哪种方案所需费用最少，最少费用是多少？

查看试题解析
28. 汛期即将来临，防汛指挥部在某水域一危险地带两岸各安置了一探照灯，便于夜间查看河水及两岸河堤的情况．如图1，灯 $A$ 射出的光束自 $A M$ 顺时针旋转至 $A N$ 便立即回转，灯 $B$ 射出的光束自 $B P$ 顺时针旋转至 $B Q$ 便立即回转，两灯不停交叉照射巡视．若灯 $A$ 射出的光束转动的速度是 $a °$ /秒，灯 $B$ 射出的光束转动的速度是 $b °$ /秒，且 $a$ 、 $b$ 满足 $| a - 3 b | + (a + b - 4)^{2} = 0$ ．假定这一带水域两岸河堤是平行的，即 $P Q / / M N$ ，且 $∠ B A N = 45 °$ ．

(1)、求 $a$ 、 $b$ 的值；

(2)、如图2，两灯同时转动，在灯 $A$ 射出的光束到达 $A N$ 之前，若两灯射出的光束交于点 $C$ ，过 $C$ 作 $C D ⊥ A C$ 交 $P Q$ 于点 $D$ ，若 $∠ B C D = 20 °$ ，求 $∠ B A C$ 的度数；

(3)、若灯 $B$ 射线先转动30秒，灯 $A$ 射出的光束才开始转动，在灯 $B$ 射出的光束到达 $B Q$ 之前， $A$ 灯转动几秒，两灯的光束互相平行?

查看试题解析