江苏省苏州市张家港市2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-24 类型:期末考试
一、单选题
-
1. 的计算结果是( )A、 B、 C、 D、x2. 如图,数轴上所表示的不等式的解集是( )
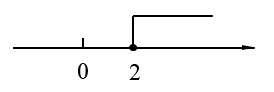 A、x≥2 B、x>2 C、x<2 D、x≤23. 某种病毒颗粒平均直径约为0.000000125,数据0.000000125用科学记数法表示为( )A、0.125× 10-6 B、1.25× 10-6 C、1.25×10-7 D、12.5×10-84. 若a<b,则下列各式中不成立的是( )A、 B、 C、 D、5. 下列各式由左边到右边的变形,属于因式分解的是( )A、 B、 C、a(x+y)=ax+ay D、6. 如图,直线ab,点A在直线a上.在ABC中,∠B=90°,∠C=25°,∠1=75°,则∠2的度数为( )
A、x≥2 B、x>2 C、x<2 D、x≤23. 某种病毒颗粒平均直径约为0.000000125,数据0.000000125用科学记数法表示为( )A、0.125× 10-6 B、1.25× 10-6 C、1.25×10-7 D、12.5×10-84. 若a<b,则下列各式中不成立的是( )A、 B、 C、 D、5. 下列各式由左边到右边的变形,属于因式分解的是( )A、 B、 C、a(x+y)=ax+ay D、6. 如图,直线ab,点A在直线a上.在ABC中,∠B=90°,∠C=25°,∠1=75°,则∠2的度数为( ) A、30° B、35° C、40° D、65°7. 如图,点C是AE中点,∠A=∠DCE,添加一个条件,不能判定ABC≌CDE的是( )
A、30° B、35° C、40° D、65°7. 如图,点C是AE中点,∠A=∠DCE,添加一个条件,不能判定ABC≌CDE的是( )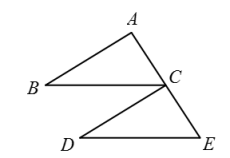 A、∠B=∠D B、AB=CD C、BCDE D、BC=DE8. 《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也为50.问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为( )A、 B、 C、 D、9. 如图,在三角形纸片ABC中, . 将三角形纸片ABC沿DE折叠,使点A落在ABC所在平面内的点处.若 , 则的度数为( )
A、∠B=∠D B、AB=CD C、BCDE D、BC=DE8. 《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也为50.问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为( )A、 B、 C、 D、9. 如图,在三角形纸片ABC中, . 将三角形纸片ABC沿DE折叠,使点A落在ABC所在平面内的点处.若 , 则的度数为( )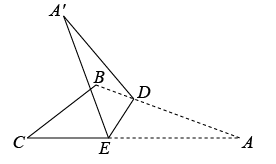 A、62.5° B、70° C、65° D、72.5°10. 如图,ABC的角平分线CD,BE相交于点F,∠BAC=∠AGB,AGBC,下列结论中不一定成立的是( )
A、62.5° B、70° C、65° D、72.5°10. 如图,ABC的角平分线CD,BE相交于点F,∠BAC=∠AGB,AGBC,下列结论中不一定成立的是( ) A、∠BAG=2∠CBE B、 C、∠AEB=∠GBE D、∠ADC=∠AEB
A、∠BAG=2∠CBE B、 C、∠AEB=∠GBE D、∠ADC=∠AEB二、填空题
-
11. 计算:4x3y·x2的结果是 .12. 若一个正多边形的一个外角等于36°,则这个正多边形的边数是.13. 如果是方程的解,则a的值为 .14. 命题“对顶角相等”的逆命题是一个命题(填“真”或“假”).15. 已知 , , 则的值为 .16. 已知 , 则的值为 .17. 如图,在ABC中,AD是中线,点E是AB中点,且 , 若AEF的面积是2,则CDF的面积为 .
 18. 在一次课外活动中,小明将一副直角三角板如图放置,E在AC上, , , . 小明将ADE从图中位置开始,绕点按每秒的速度顺时针旋转一周,在旋转过程中,第秒时,边与边平行.
18. 在一次课外活动中,小明将一副直角三角板如图放置,E在AC上, , , . 小明将ADE从图中位置开始,绕点按每秒的速度顺时针旋转一周,在旋转过程中,第秒时,边与边平行.
三、解答题
-
19. 计算:(1)、;(2)、 .20. 因式分解:(1)、;(2)、 .21. 解二元一次方程组:22. 解不等式组:23. 如图,ABC的顶点都在方格纸的格点上,其中每个格子的边长为1个单位长度.
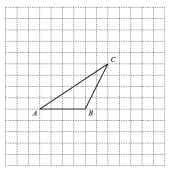
(1)将ABC先向左平移1格,再向上平移4格,在图中画出平移后的;
(2)画出ABC中AC边上的中线BD;
(3)画出ABC中AB边上的高CE;
(4)连接 , , 则四边形的面积为 .24. 如图,四边形ABCD中,BC=CD=2AB,ABCD,∠B=90°,E是BC的中点,AC与DE相交于点F. (1)、求证:ABC≌ECD;(2)、判断线段AC与DE的位置关系,并说明理由.25. 为了更好地开展劳动实践,某校在校园内开辟了一片小菜园.初一年级组想要购进A、B两种蔬菜苗进行种植.若购进A种蔬菜苗7棵,B种蔬菜苗3棵,需要85元;若购进A种蔬菜苗3棵,B种蔬菜苗6棵,需要60元.(1)、购进A、B两种蔬菜苗每棵各需多少元?(2)、若初一年级组决定购进这两种蔬菜苗共100棵,且用于购买这100棵蔬菜苗的资金不超过765元,那么初一年级组最多可以购进A种蔬菜苗多少棵?26. 已知关于x,y的二元一次方程组(m是常数).(1)、若方程组的解满足 , 求m的值;(2)、若方程组的解满足 , 求m的取值范围.27. 利用我们学过的完全平方公式及不等式知识能解决方程或代数式的一些问题,请阅读下列材料:
(1)、求证:ABC≌ECD;(2)、判断线段AC与DE的位置关系,并说明理由.25. 为了更好地开展劳动实践,某校在校园内开辟了一片小菜园.初一年级组想要购进A、B两种蔬菜苗进行种植.若购进A种蔬菜苗7棵,B种蔬菜苗3棵,需要85元;若购进A种蔬菜苗3棵,B种蔬菜苗6棵,需要60元.(1)、购进A、B两种蔬菜苗每棵各需多少元?(2)、若初一年级组决定购进这两种蔬菜苗共100棵,且用于购买这100棵蔬菜苗的资金不超过765元,那么初一年级组最多可以购进A种蔬菜苗多少棵?26. 已知关于x,y的二元一次方程组(m是常数).(1)、若方程组的解满足 , 求m的值;(2)、若方程组的解满足 , 求m的取值范围.27. 利用我们学过的完全平方公式及不等式知识能解决方程或代数式的一些问题,请阅读下列材料:阅读材料:若 , 求m、n的值.
解:∵ , ∴ ,
∴ , ∴ , , ∴ , .
根据你的观察,探究下面的问题:
(1)、已知 , 求 , ;(2)、已知ABC的三边长a、b、c都是正整数,且满足 , 求c的值;(3)、若 , 试比较A与B的大小关系,并说明理由.28. 如图,∠MAN是一个钝角,AB平分∠MAN,点C在射线AN上,且AB=BC,BD⊥AC,垂足为D.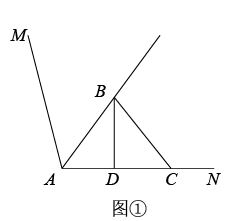
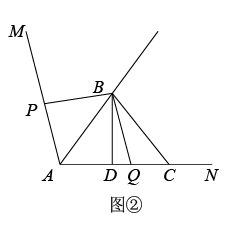
 (1)、求证:;(2)、动点P,Q同时从A点出发,其中点Q以每秒3个单位长度的速度沿射线AN方向匀速运动;动点P以每秒1个单位长度的速度匀速运动.已知AC=5,设动点P,Q的运动时间为t秒.
(1)、求证:;(2)、动点P,Q同时从A点出发,其中点Q以每秒3个单位长度的速度沿射线AN方向匀速运动;动点P以每秒1个单位长度的速度匀速运动.已知AC=5,设动点P,Q的运动时间为t秒.①如图②,当点P在射线AM上运动时,若点Q在线段AC上,且 , 求此时t的值;
②如图③,当点P在直线AM上运动时,点Q在射线AN上运动的过程中,是否存在某个时刻,使得APB与BQC全等?若存在,请求出t的值;若不存在,请说出理由.