江苏省苏州市相城区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-24 类型:期末考试
一、单选题
-
1. 下列运算中,正确的是( )A、 B、 C、 D、2. 已知三角形的两边长分别为2cm和3cm,则该三角形第三边的长不可能是( )A、1cm B、2cm C、3cm D、4cm3. 若是二元一次方程的一个解,则下列x,y的值也是该方程的解的是( )A、 B、 C、 D、4. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、5. 如图,直线 , 将含30°角的直角三角板ABC的直角顶点C放在直线b上,若 , 则的度数为( )
 A、35° B、45° C、55° D、65°6. 用直尺和圆规作一个角等于已知角,如图,要证 , 则只需证明 , 依据是( )
A、35° B、45° C、55° D、65°6. 用直尺和圆规作一个角等于已知角,如图,要证 , 则只需证明 , 依据是( ) A、SAS B、SSS C、AAS D、ASA7. 如图,在中, , , BD平分 , 于点E,则的度数为( )
A、SAS B、SSS C、AAS D、ASA7. 如图,在中, , , BD平分 , 于点E,则的度数为( )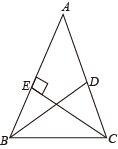 A、90° B、100° C、110° D、120°8. 若 , , 则等于( )A、 B、 C、 D、9. 若 , 那么代数式的值为( )A、 B、 C、1 D、310. 若关于x的不等式组的解集是 , 则a的取值范围是( )A、 B、 C、 D、
A、90° B、100° C、110° D、120°8. 若 , , 则等于( )A、 B、 C、 D、9. 若 , 那么代数式的值为( )A、 B、 C、1 D、310. 若关于x的不等式组的解集是 , 则a的取值范围是( )A、 B、 C、 D、二、填空题
-
11. “墙角数枝梅,凌寒独自开.遥知不是雪,为有暗香来.”出自宋代诗人王安石的《梅花》.梅花的花粉直径约为0.000036m,用科学记数法表示该数据为 .12. 计算的结果等于 .13. 若多边形的内角和比外角和大540°,则该多边形的边数是 .14. 命题“如果 , 那么”是命题.(选填“真”或“假”)15. 如图,小明在用量角器度量的大小时,将边OB放在0刻度线上,但是顶点O放在中心点的右侧,此时边OA过50°刻度线,则50°.(选填“<”,“=”或“>”)
 16. 如图,已知 , 点D,E分别在AB,AC上,且 , , , 则的度数是 .
16. 如图,已知 , 点D,E分别在AB,AC上,且 , , , 则的度数是 .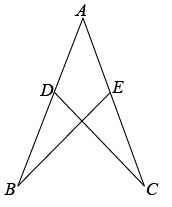 17. 若 , 且 , 则x的取值范围为 .18. 如图,在中,AD为的平分线,于E,连接CE,若的面积为 , 则的面积为 .
17. 若 , 且 , 则x的取值范围为 .18. 如图,在中,AD为的平分线,于E,连接CE,若的面积为 , 则的面积为 .
三、解答题
-
19. 计算:(1)、(2)、20. 分解因式:(1)、(2)、21. 解方程组:22. 解不等式组,并在数轴上表示解集:23. 如图,在的长方形网格中,每个小正方形的边长均为1,小正方形的每一个顶点叫做格点,线段DE和三角形ABC的顶点都在格点上.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
 (1)、的面积为 .(2)、在DE的右侧找一点F,使得与全等;(3)、画中BC边上的高AH.24. 如图,在四边形ABCD中, , , E,F是对角线AC上两点,且 , 连接BE,DF.
(1)、的面积为 .(2)、在DE的右侧找一点F,使得与全等;(3)、画中BC边上的高AH.24. 如图,在四边形ABCD中, , , E,F是对角线AC上两点,且 , 连接BE,DF.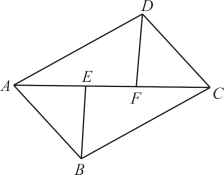 (1)、求证:;(2)、若 , 求的度数.25. 已知关于x,y的方程组(1)、当时,求m的值;(2)、若x为非负数,y为负数,求m的取值范围.26. 某汽车专卖店销售A,B两种型号的新能源汽车.第一周售出1辆A型车和3辆B型车,销售额为96万元;第二周售出2辆A型车和1辆B型车,销售额为62万元.(1)、求每辆A型车和B型车的售价各为多少万元?(2)、某公司准备花540万元购进A,B两种型号的新能源汽车不超过25台,问两种型号的车各购买多少台?27. 【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到 , 基于此,请解答下列问题;
(1)、求证:;(2)、若 , 求的度数.25. 已知关于x,y的方程组(1)、当时,求m的值;(2)、若x为非负数,y为负数,求m的取值范围.26. 某汽车专卖店销售A,B两种型号的新能源汽车.第一周售出1辆A型车和3辆B型车,销售额为96万元;第二周售出2辆A型车和1辆B型车,销售额为62万元.(1)、求每辆A型车和B型车的售价各为多少万元?(2)、某公司准备花540万元购进A,B两种型号的新能源汽车不超过25台,问两种型号的车各购买多少台?27. 【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到 , 基于此,请解答下列问题;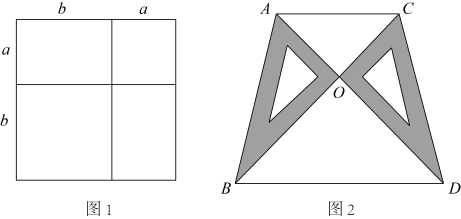 (1)、【直接应用】若 , , 求xy的值;(2)、【类比应用】填空:①若 , 则 ▲ ;
(1)、【直接应用】若 , , 求xy的值;(2)、【类比应用】填空:①若 , 则 ▲ ;②若 , 则 ▲ ;
(3)、【知识迁移】两块全等的特制直角三角板()如图2所示放置,其中A,O,D在一直线上,连接AC,BD.若 , , 求一块直角三角板的面积.28. 已知:如图1, , BD平分 , , 过点A作直线 , 延长CD交MN于点E
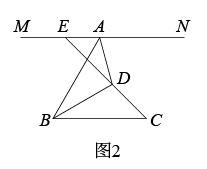 (1)、当时,的度数为 .(2)、如图2,当时,求的度数;(3)、设 , 用含x的代数式表示的度数.
(1)、当时,的度数为 .(2)、如图2,当时,求的度数;(3)、设 , 用含x的代数式表示的度数.