江苏省连云港市海州区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-24 类型:期末考试
一、单选题
-
1. 下列各方程中是二元一次方程的是( )A、=﹣1 B、xy+z=5 C、2x2+3y﹣5=0 D、2x+=22. 每到四月,许多地方杨絮、柳絮如雪花漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为m,该数值用科学记数法表示为( )A、 B、 C、 D、3. 如果a>b,那么下列不等式成立的是( )A、a﹣b<0 B、a﹣3<b﹣3 C、 D、﹣3a<﹣3b4. 如图,下列条件中,不能判断直线 的是( )
 A、 B、 C、 D、5. 不等式2x+3≥5的解集在数轴上表示正确的是( )
A、 B、 C、 D、5. 不等式2x+3≥5的解集在数轴上表示正确的是( )
A、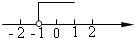 B、
B、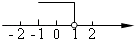 C、
C、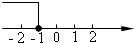 D、
D、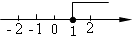 6. 我校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人,设运动员人数为人,组数为组,则列方程组为( )A、 B、 C、 D、7. 如图是长方形纸带, , 将纸带沿折叠成图 , 再沿折叠成图 , 则图中的的度数是( )
6. 我校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人,设运动员人数为人,组数为组,则列方程组为( )A、 B、 C、 D、7. 如图是长方形纸带, , 将纸带沿折叠成图 , 再沿折叠成图 , 则图中的的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 若 , 则 .9. 如果三条线段长度为 , 1,3(为整数),且这三条线段能首尾依次相接组成三角形,那么的值为 .10. 一个多边形的每一个外角都等于60°,则这个多边形的内角和为 度.11. 命题:“如果a=b,那么a2=b2”的逆命题是命题(填“真”或“假”).12. 如果关于x的不等式 的解集为 ,写出一个满足条件的a值13. 已知 , 且 , 那么的取值范围为 .14. 如图,AB∥CD,一副三角尺按如图所示放置,∠AEG=20°,则∠HFD为°.
 15. 如图,长方形ABCD的周长为12,分别以BC和CD为边向外作两个正方形,且这两个正方形的面积和为20,则长方形ABCD的面积是.
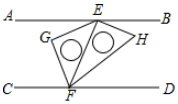
15. 如图,长方形ABCD的周长为12,分别以BC和CD为边向外作两个正方形,且这两个正方形的面积和为20,则长方形ABCD的面积是. 16. 如图,四边形中, , , 点、分别在、上,将沿翻折,得 . 若 , , 则的度数为 .
16. 如图,四边形中, , , 点、分别在、上,将沿翻折,得 . 若 , , 则的度数为 . 17. 若关于的不等式组有解,且关于的方程有非负整数解,则符合条件的所有整数的和为 .
17. 若关于的不等式组有解,且关于的方程有非负整数解,则符合条件的所有整数的和为 .三、解答题
-
18. 将下列各式因式分解:(1)、 .(2)、 .19. 计算下列各题:(1)、 .(2)、先化简,再求值: , 其中 , .20.(1)、 (代入法)(2)、 (加减法)21. 解不等式(或不等式组):(1)、解不等式(2)、解不等式组22. 某隧道长1200 m,现有一列火车从隧道通过,测得该火车从开始进隧道到完全出隧道共用了70s,整列火车完全在隧道里的时间是50s,求火车的速度和长度.23. 已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H.试说明:CD⊥AB.
 24. 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}==;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=
24. 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}==;min{﹣1,2,3}=﹣1;min{﹣1,2,a}=解决下列问题:
(1)、若min{2,2x+2,4﹣2x}=2,则x的范围;(2)、①如果M{2,x+1,2x}=min{2,x+1,2x},求x;②根据①,你发现了结论“如果M{a,b,c}=min{a,b,c},那么 ▲ (填a,b,c的大小关系)”.
③运用②的结论,若M{2x+y+2,x+2y,2x﹣y}=min{2x+y+2,x+2y,2x﹣y},求x+y的值.
25. 某地区为绿化环境,计划购买甲、乙两种树苗共计棵.有关甲、乙两种树苗的信息如图所示.信 息
1.甲种树苗每棵60元;
2.乙种树苗每棵90元;
3.甲种树苗的成活率为;
4.乙种树苗的成活率为 .
(1)、当n=400时,如果购买甲、乙两种树苗共用27000元,那么甲、乙两种树苗各买了多少棵?(2)、实际购买这两种树苗的总费用恰好为27000元,其中甲种树苗买了棵.①写出与满足的关系式;
②要使这批树苗的成活率不低于 , 求的最大值.
26. 如图1,直线与直线相交于点 , 、两点同时从点出发,点以每秒个单位长度沿直线向左运动,点以每秒个单位长度沿直线向上运动. (1)、若运动时,点比点多运动1个单位;运动时,点与点运动的路程和为6个单位,则 , .(2)、如图2,当直线m与直线n垂直时,设∠BAO和∠ABO的角平分线相交于点P.点A、B在运动的过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值(写出主要过程);若发生变化,请说明理由.(3)、如图3,将(2)中的直线不动,直线绕点按顺时针方向旋转 , 其他条件不变.
(1)、若运动时,点比点多运动1个单位;运动时,点与点运动的路程和为6个单位,则 , .(2)、如图2,当直线m与直线n垂直时,设∠BAO和∠ABO的角平分线相交于点P.点A、B在运动的过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值(写出主要过程);若发生变化,请说明理由.(3)、如图3,将(2)中的直线不动,直线绕点按顺时针方向旋转 , 其他条件不变.(i)用含有的式子表示的度数 .
(ii)如果再分别作的两个外角 , 的角平分线相交于点 , 并延长、交于点 . 则下列结论正确的是(填序号).
①与互补;②为定值;③为定值;④与互余.