江苏省连云港市东海县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 2022年，中国举办了第二十四届冬季奥林匹克运动会，如图，通过平移吉祥物“冰墩墩”可以得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. 若 $a > b$ ，则下列不等式不一定成立的是（）

A、 $a + 2022 > b + 2022$ B、 $a (m^{2} + 2022) > b (m^{2} + 2022)$ C、 $- \frac{a}{2022} < - \frac{b}{2022}$ D、 $| a | > | b |$

查看试题解析
3. 下列运算错误的是（）

A、 ${(3 a)}^{2} = 6 a^{2}$ B、 $2 a \cdot 3 a = 6 a^{2}$ C、 $x^{3} \div x^{2} = x$ D、 $- x + 2 x = x$

查看试题解析
4. 下面的多项式中，能因式分解的是（）

A、 $m^{2} + n$ B、 $m^{2} - 2 m + 1$ C、 $m^{2} - n$ D、 $m^{2} - m + 1$

查看试题解析
5. $5^{- 3}$ 可以表示为（）

A、 $(- 3) \times (- 3) \times (- 3) \times (- 3) \times (- 3)$ B、 $\frac{1}{5 \times 5 \times 5}$ C、 $- 5 \times 5 \times 5$ D、 $(- 3) + (- 3) + (- 3) + (- 3) + (- 3)$

查看试题解析
6. 如图，直线a、b被直线c所截，下列说法正确的是（）

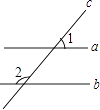A、当∠1=∠2时，一定有a∥b B、当a∥b时，一定有∠1=∠2 C、当a∥b时，一定有∠1+∠2=90° D、当∠1+∠2=180°时，一定有a∥b

查看试题解析
7. 某人分两次在市场上买了同一批货物，第一次买了3件，平均价格为每件a元，第二次买了2件，平均价格为每件b元．后来他以每件 $\frac{a + b}{2}$ 元的价格全部卖出，结果发现自己赔钱了，赔钱的原因是（）

A、 $a = b$ B、 $a > b$ C、 $a < b$ D、 $a \geq b$

查看试题解析
8. 中国古代数学著作《算法统宗》中记载了这样一个题目：九百九十九文钱，甜果苦果买一千，四文钱买苦果七，十一文钱九个甜，甜苦两果各几个？其大意是：用九百九十九文钱共买了一千个苦果和甜果，其中四文钱可以买苦果七个，十一文钱可以买甜果九个．问：苦、甜果各有几个？设苦果有 $x$ 个，甜果有 $y$ 个，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 1000 \\ \frac{4}{7} x + \frac{11}{9} y = 999 \end{array}$ B、 ${\begin{array}{l} x + y = 1000 \\ \frac{7}{4} x + \frac{9}{11} y = 909 \end{array}$ C、 ${\begin{array}{l} x + y = 1000 \\ 7 x + 9 y = 999 \end{array}$ D、 ${\begin{array}{l} x + y = 1000 \\ 4 x + 11 y = 999 \end{array}$

查看试题解析

二、填空题

9. 计算 ${(- 2022)}^{0}$ 的结果是．

查看试题解析
10. 俗话说：“水滴石穿”，水滴不断地落在一块石头的同一个位置，经过几年后，石头上形成了一个深度为0.0039毫米的小洞，数据0.0039用科学记数法表示为．

查看试题解析
11. “如果 $a^{2} > b^{2}$ ，那么 $a > b$ ”是假命题，请举出一个反例．在你举出的反例中， $a =$ ， $b =$ ．

查看试题解析
12. 已知一个多边形的每一个内角都等于150°，则这个多边形的边数是．

查看试题解析
13. 若 $(x + 1) (x^{2} - 5 a x + a)$ 的乘积中不含 $x^{2}$ 项，则a的值为．

查看试题解析
14. 已知x＝2﹣t，y＝3t﹣1，用含x的代数式表示y，可得y= ．

查看试题解析
15. 三角形三边长分别为3， $2 a - 1$ ， $4.$ 则a的取值范围是．

查看试题解析

16. 工作人员从仓库领取如图①中的长方形和正方形纸板作侧面和底面，做成如图②的竖式和横式的两种无盖纸盒若干个，恰好使领取的纸板用完．

下表是工作人员四次领取纸板数的记录：

日期	正方形纸板（张）	长方形纸板（张）
第一次	356	544
第二次	422	860
第三次	500	1000
第四次	988	2022

仓库管理员在核查时，发现一次记录有误．则记录有误的是第次．

查看试题解析

三、解答题

17. 计算：

(1)、 $m^{3} \cdot m \cdot {(m^{2})}^{3}$ ；

(2)、 $(a + 9) (a + 1)$ ．

查看试题解析
18. 分解因式：

(1)、 $12 x y z - 9 x^{2} y$ ；

(2)、 $4 x^{2} - 64$ ．

查看试题解析
19. 先化简，再求值： $(3 a + 1) (3 a - 1) - 9 a (a - 1)$ ，其中 $a = 2$ ．

查看试题解析
20. 解下列方程组：

(1)、 ${\begin{array}{l} x = y - 3 \\ 7 x + 5 y = 9 \end{array}$

(2)、 ${\begin{array}{l} \frac{1}{2} x + 3 y = - 6 \\ \frac{1}{2} x + y = 2 \end{array}$

查看试题解析
21. 解不等式（组）：

(1)、 $x - 2 (x - 1) > 0$

(2)、 ${\begin{array}{l} 4 x - 3 < 5 x \\ \frac{x - 4}{2} + \frac{x + 2}{6} \leq \frac{1}{3} \end{array}$

查看试题解析
22. 如图，网格中最小正方形的边长为1， $△ A B C$ 的顶点都在格点上．根据下列条件，利用网格点和直尺画图或计算：

(1)、画出AC边上的中线BD；

(2)、 $△ A B D$ 的面积为；

(3)、在图中能使 $S_{△ P A C} = S_{△ A B C}$ 的格点P的个数有个（点P异于点B）．

查看试题解析
23. 如图， $∠ A B E$ 是四边形ABCD的外角，已知 $∠ A B E = ∠ D$ ．
求证： $∠ A + ∠ C = 180 °$

查看试题解析
24. 完成下面的证明：
已知：如图， $A C ∥ D E$ ， CD平分 $∠ A C B$ ， EF平分 $∠ D E B$ ．
求证： $C D ∥ E F$ ．
证明：∵ $A C ∥ D E$ ，
∴ $∠ A C B = ∠$   ▲  （  ）．
∵CD平分 $∠ A C E$ ， EF平分 $∠ D E B$ ，
∴∠1=  ▲   ， ∠2=  ▲   ．
∴∠  ▲  =∠  ▲   ．
∴ $C D ∥ E F$ （  ）．

查看试题解析
25. 某货运公司有大小两种货车，3辆大货车与4辆小货车一次可以运货29吨，2辆大货车与6辆小货车一次可以运货31吨.

(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨；

(2)、目前有46.4吨货物需要运输，货运公司拟安排大小货车共10辆，全部货物一次运完，其中每辆大货车一次运货花费500元，每辆小货车一次运货花费300元，请问货运公司应如何安排车辆最节省费用？最低费用为多少？

查看试题解析
26. 完全平方公式 ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 进行适当的变形后，可以解决很多的数学问题．
如：若x满足 $(9 - x) (x - 4) = 4$ ，求 ${(9 - x)}^{2} + {(x - 4)}^{2}$ 的值．

解题思路：由 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 得 $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b$ ，

可设 $9 - x = a$ ， $x - 4 = b$ ，则 $(9 - x) (x - 4) = a b = 4$ ， $a + b = (9 - x) + (x - 4) = 5$ ，

∴ ${(9 - x)}^{2} + {(x - 4)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 5^{2} - 2 \times 4 = 17$ ；

(1)、请仿照上面的方法求解下面问题：
①若x满足 $(6 - x) (x - 2) = 2$ ，求 ${(6 - x)}^{2} + {(x - 2)}^{2}$ 的值；

②若x满足 $(6 + x) (2 + x) = 5$ ，求 ${(6 + x)}^{2} + {(2 + x)}^{2}$ 的值；

(2)、应用上面的解题思路解决问题：如图，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设 $A B = 8$ ，两正方形的面积和 $S_{1} + S_{2} = 34$ ，求图中阴影部分的面积．

查看试题解析
27. 【原题重现】
课本第154页例2：如图1，AC、BD相交于点O，求证： $∠ A + ∠ B = ∠ C + ∠ D$ ．

某数学兴趣小组同学对此题展开了探究讨论．

(1)、【解法再探】
课本利用“三角形内角和是180°”和“对顶角相等”对此题进行了证明，小明同学提出了另外一种证明方法，如下思路框图：

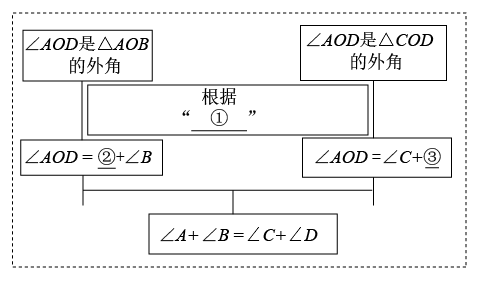
完成框图填空：① ， ② ， ③；

(2)、【变式拓展】
小慧同学把图1中线段AC与BD相交所组成的结构称为“8字形”，她对原题进行了改编：如图2，AC、BD相交于点O，∠BAC、∠BDC的角平分线交于点P， $∠ B = α$ ， $∠ C = β$ ，求∠P的度数（用含 $α$ ， $β$ 的式子表示）．请你帮助小明完成以下问题：

小明看到图2中有两个与∠P相关的“8字形”，请你根据（1）的结论写出关于∠P的两个关系式为：① $∠ P + ∠ B D P =$ ；② $∠ P + ∠ C A P =$ ；

小明进一步思考：设 $∠ B A C = x$ ， $∠ B D C = y$ ，由 $∠ A + ∠ B = ∠ C + ∠ D$ ，得 $x + α = β + y$ ， ③ $x - y = β - α$ ，由①、③（或②、③）联立、转化、整理可得结论： $∠ P =$ ；

(3)、【发现生成】
小慧同学为了寻找规律，再次改变条件：如图3，AC、BD相交于点O， $∠ B A P = \frac{1}{3} ∠ B A C$ ， $∠ B D P = \frac{1}{3} ∠ B D C$ ， $∠ B = α$ ， $∠ C = β$ ，求 $∠ P$ 的度数（用含 $α$ ， $β$ 的式子表示）．请你写出解答：

(4)、若把（3）中的“ $\frac{1}{3}$ ”都改为“ $\frac{1}{n}$ ”，则 $∠ P =$ ．（用含 $α$ ， $β$ 的式子表示）

查看试题解析