江苏省淮安市盱眙县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2022-08-24 类型:期末考试
一、单选题
-
1. 若一个三角形的两边长分别为3cm和7cm,则第三边长可能是( )A、4cm B、9cm C、10cm D、11cm2. 下列计算正确的是( )A、 B、 C、 D、3. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片,该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为( )A、 B、 C、 D、4. 下列命题为假命题的是( )A、若|a|=|b|,则a=b B、两直线平行,内错角相等, C、对顶角相等 D、若a=0,则ab=05. 已知是二元一次方程的一个解,则a的值为( )A、2 B、-2 C、-1 D、46. 如图,直线// , 则的度数是( )
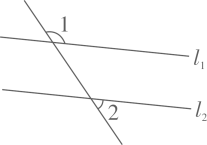 A、30° B、40° C、50° D、65°7. 不等式2x+3>1的解集在数轴上表示正确的是( )A、
A、30° B、40° C、50° D、65°7. 不等式2x+3>1的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、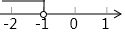 D、
D、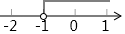 8. 如图,在中, , 点D在AB上,将沿CD折叠,点B落在边AC的点E处.若 , 则的度数为( )
8. 如图,在中, , 点D在AB上,将沿CD折叠,点B落在边AC的点E处.若 , 则的度数为( )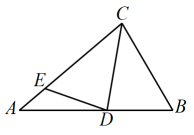 A、24° B、32° C、38° D、48°
A、24° B、32° C、38° D、48°二、填空题
-
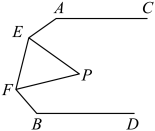
9. 计算的结果是 .10. 分解因式: .11. 已知一个正多边形的一个内角是120º,则这个多边形的边数是 .12. 写出二元一次方程的一组正整数解为 .13. 命题“对顶角相等”的逆命题是一个命题(填“真”或“假”).14. 若x+y=2,xy=-1,则x2+y2= .15. 已知 , 则.16. 如图,// , EP、FP分别平分、 , 若 , 则°.(用含m,n的代数式表示)
三、解答题
-
17. 计算:(1)、;(2)、 .18.(1)、解方程组(2)、解不等式组19. 先化简,再求值: , 其中 .20. 如图,在方格纸内将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
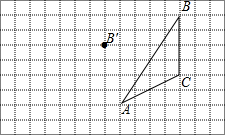 (1)、补全△A′B′C′;(2)、画出AC边上的中线BD;(3)、求△ABD的面积 .21. 已知:如图,BC∥AE,∠C=∠A,求证:CD∥AF.
(1)、补全△A′B′C′;(2)、画出AC边上的中线BD;(3)、求△ABD的面积 .21. 已知:如图,BC∥AE,∠C=∠A,求证:CD∥AF.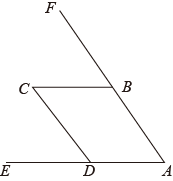 22. 如图,AD、BE分别是的高和角平分线, , 求的度数.
22. 如图,AD、BE分别是的高和角平分线, , 求的度数.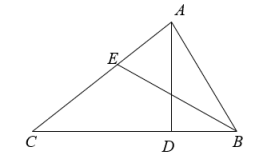 23. 如图所示,直角梯形ABCD中,O是BC的中点,求的面积(用含a,b的式子表示).
23. 如图所示,直角梯形ABCD中,O是BC的中点,求的面积(用含a,b的式子表示).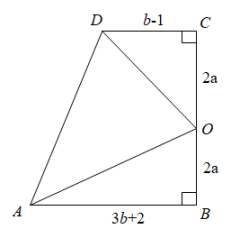 24. 已知 .(1)、请用含x的式子表示y;(2)、当时,求x的最大值.25. 某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨;(2)、目前有46.4吨货物需要运输,货运公司拟安排大小货车共10辆,全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?最低费用为多少?26. 已知 , 点A在射线CE上,把沿AB翻折得 , .
24. 已知 .(1)、请用含x的式子表示y;(2)、当时,求x的最大值.25. 某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨;(2)、目前有46.4吨货物需要运输,货运公司拟安排大小货车共10辆,全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?最低费用为多少?26. 已知 , 点A在射线CE上,把沿AB翻折得 , . (1)、若 , 则的度数为°;(2)、设 , ,
(1)、若 , 则的度数为°;(2)、设 , ,①如图1,当点D在直线CE左侧时,求y与x的数量关系,并写出x的取值范围;
②如图2,当点D在直线CE右侧时出y与x的数量关系是 ▲ ;
(3)、过点D作//交CE于点F,当时,求的度数.27.(1)、学习“完全平方公式”时,小明遇到课本上一道题目“计算”,他联系所学过的知识和方法,想到两种解决思路;①可以用“整体思想”把三项式转化为两部分:或 , 然后可以利用完全平方公式解决,请你选择一种变形方法写出计算过程.
②可以用“数形结合”的方法,画出表示的图形,根据面积关系得到结果.请你在下面方框中画出图形,并作适当标注.
 (2)、利用(1)的结论分解因式: .(3)、小明根据“任意一个数的平方不小于0”,利用配方法求出了一些二次多项式的最大值或最小值,方法如下:
(2)、利用(1)的结论分解因式: .(3)、小明根据“任意一个数的平方不小于0”,利用配方法求出了一些二次多项式的最大值或最小值,方法如下:①
∵
∴ .
故当时代数式的最小值为-2
②
∵
∴
故当时代数式的最大值为4
请你参考小明的方法,求当x,y取何值时代数式有最小值,并确定它的最小值.