江苏省常州市教育学会2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 能使不等式x＋1>3成立的x的值是（）

A、－3 B、－1 C、2 D、4

查看试题解析
2. 下列计算中，一定正确的是（）

A、 $x + x^{2} = x^{3}$ B、 $x \cdot x^{2} = x^{3}$ C、 ${(x^{3})}^{2} = x^{5}$ D、 $\frac{x^{6}}{x^{2}} = x^{3}$

查看试题解析
3. 下列命题中，真命题是（）

A、如果a＋b＝0，那么 $| a | = | b |$ B、两个锐角的和是钝角 C、如果一点到线段两端的距离相等，那么这点是这条线段的中点 D、任何数的平方都大于0

查看试题解析
4. 现有方程组 ${\begin{array}{l} x - y = m ， \\ 2 x + 3 y = 3 m + 1 \end{array}$ ，消去m，得x与y的关系式为（）

A、3x＋2y＝1 B、x＋4y＝1 C、5x＋6y＝1 D、x－6y＝－1

查看试题解析
5. 如图，AD是△ABC的中线，点E在线段AD上，且 $D E = \frac{1}{2} A E$ ．若△DEC的面积是1，则△ABD的面积是（）

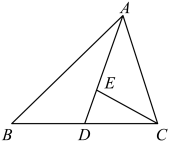A、2 B、3 C、4 D、6

查看试题解析
6. 《算法统宗》中有一道题为“隔沟计算”，其原文是：甲乙隔沟放牧，二人暗里参详，甲云得乙九只羊，多你一倍之上；乙说得甲九只羊，二家之数相当，两人闲坐恼心肠，画地算了半晌．这个题目的意思是：甲、乙两个牧人隔着山沟放羊，两人都在暗思对方有多少只羊，甲对乙说：“我若得你9只羊，我的羊多你一倍．”乙对甲说：“我若得你9只羊，我们两家的羊数就一样多．”设甲有x只羊，乙有y只羊，根据题意列出二元一次方程组为（）

A、 ${\begin{array}{l} x - 9 = 2 (y + 9) ， \\ y + 9 = x - 9 . \end{array}$ B、 ${\begin{array}{l} x + 9 = 2 (y - 9) ， \\ y + 9 = x - 9 . \end{array}$ C、 ${\begin{array}{l} x + 9 = 2 y ， \\ y + 9 = x . \end{array}$ D、 ${\begin{array}{l} x - 9 = 2 y ， \\ y + 9 = x - 9 . \end{array}$

查看试题解析
7. 甲、乙、丙3人从图书馆各借了一本书（如下表所示），他们相约在每个星期天相互交换读完的书，经过数次交换后，他们都读完了这3本书．已知甲读的第三本书是乙读的第二本书，则丙读的第二本书是（）
甲
乙
丙
书A
书B
书C

A、书A B、书B C、书C D、无法确定

查看试题解析
8. 把一副三角尺按如图所示放置（2个直角顶点重合），则∠1、∠2、∠3的和是（）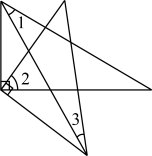

A、60° B、90° C、105° D、120°

查看试题解析

二、填空题

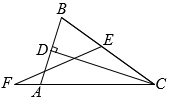
9. 若a>b，则2a－32b－3（用“>”或“<”填空）．

查看试题解析
10. 命题“正整数是自然数”的逆命题是．

查看试题解析
11. 2022年北京冬奥会赛事场地之一的张家口万龙滑雪场的雪几乎都是人造雪，人造雪的制造过程为：首先用直径为0.00003~0.00007米的水滴制造微小的冰晶，它们就是晶核，接着向外喷射晶核，让水雾和晶核接触，形成雪花．数据0.00003用科学记数法表示为．

查看试题解析
12. 已知 ${\begin{array}{l} x = 1 ， \\ y = 1 \end{array}$ 是方程组 ${\begin{array}{l} a x - b y = 1 ， \\ a x + b y = 3 \end{array}$ 的解，则 $a^{2} - b^{2} =$ ．

查看试题解析
13. 两根木棒分别长4cm、6cm，第三根木棒与这两根木棒首尾依次相接构成三角形．已知第三根木棒的长为奇数（单位：cm），则一共可以构成个不同的三角形．

查看试题解析
14. 已知 $2^{x + y} = 1$ ，且－1<x<2，则y的取值范围是．

查看试题解析
15. 在一个多边形中，小于72°的内角最多有个．

查看试题解析
16. 如图，CD是△ABC的高，且CD平分∠ACB，∠BAC＝70°，∠CFE＝25°，则∠CEF＝°．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(- 2022)}^{0} - {(\frac{1}{2})}^{- 2} + {(- 2)}^{3}$ ；

(2)、 ${(3 a - b)}^{2} - (a - 3 b) (a + 3 b)$ ．

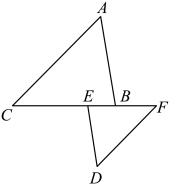
查看试题解析
18. 分解因式：

(1)、 $2 x^{2} - 32$ ；

(2)、 $x^{3} y + 2 x^{2} y^{2} + x y^{3}$ ．

查看试题解析
19. 解方程组或不等式组：

(1)、 ${\begin{array}{l} 2 x + 3 y = 5 \\ x + y = 2 \end{array}$

(2)、 ${\begin{array}{l} 3 x + 4 > 7 \\ 4 x - 2 < 3 x \end{array}$

查看试题解析
20.

(1)、已知x＋y＝3，xy＝2．求 $x^{2} + y^{2}$ 、 ${(x - y)}^{2}$ 的值；

(2)、已知x＋2y＝3，xy＝1．求 $x^{2} - x y + 4 y^{2}$ 的值．

查看试题解析
21. 已知：如图，点C、E、B、F在一条直线上， $A C ∥ F D$ ， ∠A＝∠D．
求证： $A B ∥ D E$ ．

查看试题解析
22. 某商店分别以标价的8折和9折销售A、B两种品牌的衬衫各1件，共收款364元．已知这两件衬衫标价的和为420元．

(1)、这两件衬衫的标价各为多少元？

(2)、若按标价销售这两种品牌的衬衫共10件，总收款不低于2500元，则销售B品牌的衬衫最少多少件？

查看试题解析
23. 在如图的网格中，A、B、C、E、F为格点，点P在线段EF上．

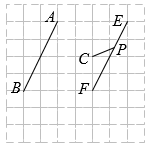(1)、线段AB向右平移格可以得到线段EF；

(2)、过点C画AB的垂线，垂足为D；

(3)、若 $∠ C P E = α °$ ，则∠DCP＝°．（用含 $α$ 的代数式表示）．

查看试题解析
24. 如图，现有两张长方形纸片A、B．

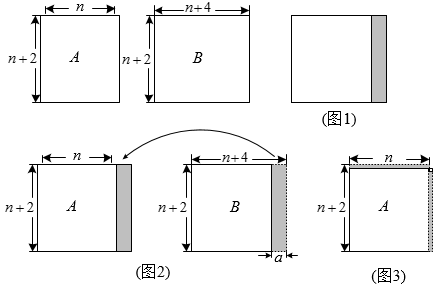(1)、将两张纸片按图1所示叠合，可得阴影部分的面积即为两张纸片的面积差．若两张纸片的面积差大于90，求n的最小整数值；

(2)、如图2，将纸片B剪下一个小长方形，并将其与纸片A拼接，得到两个一样的正方形，则图中的a＝；由纸片的总面积保持不变，可得等式： $n (n + 2) + (n + 2) (n + 4) = 2 {(______)}^{2}$ ；

(3)、如图3，将纸片A剪拼，再添加一个小正方形，得到一个大正方形．根据这一过程，可得等式： $n (n + 2) +______= {(______)}^{2}$ ．

查看试题解析
25. 如果两个角的差等于30°，就称这两个角互为“伙伴角”，其中一个角叫做另一个角的“伙伴角”．例如 $α = 70 °$ ， $β = 40 °$ ， $α - β = 30 °$ ，则 $α$ 和 $β$ 互为“伙伴角”，即 $α$ 是 $β$ 的“伙伴角”， $β$ 也是 $α$ 的“伙伴角”．

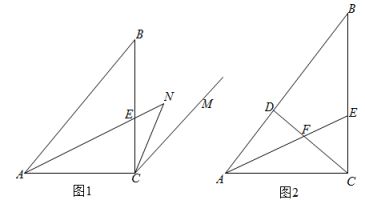(1)、已知∠1和∠2互为“伙伴角”，∠1>∠2，且∠1和∠2互补，求∠1的度数；

(2)、在△ABC中，∠ACB＝90°，AE是角平分线．
①如图1，过点C作AB的平行线CM，射线CN平分∠BCM，且与射线AE交于点N．若∠ANC与∠ABC互为“伙伴角”，则∠ABC＝ ▲ ；
②如图2，过点C作AB的垂线，垂足为D，AE、CD相交于点F．若∠FCE与∠CEF互为“伙伴角”，求∠ABC的度数．

查看试题解析

甲	乙	丙
书A	书B	书C