湖南省长沙市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、3 B、 $\pm 3$ C、 $- 3$ D、9

查看试题解析
2. 若 $m > n ，$ 则下列不等式不一定成立的是（）

A、 $m + 2 > n + 2$ B、 $- 2 m < - 2 n$ C、 $\frac{m}{2} > \frac{n}{2}$ D、 $m^{2} > n^{2}$

查看试题解析
3. 如图，直线AB与CD相交于点O， $∠ A O C = 75 °$ ， $∠ 1 = 25 °$ ，则 $∠ 2$ 的度数是（）

A、25° B、30° C、40° D、50°

查看试题解析
4. 把不等式组 ${\begin{cases} x > - 1 \\ x \leq 1 \end{cases}$ 的解集表示在数轴上，正确的是（　　）

A、 B、 C、 D、

查看试题解析
5. 今年长沙市大约有4万名学生参加中考，为了了解这些考生的数学成绩，从中抽取1200名考生的数学成绩进行统计分析．在这个问题中，有下列四种说法：
①这4万名考生的数学中考成绩的全体是总体；
②每个考生是个体；
③1200名考生是总体的一个样本；
④样本容量是1200．
其中说法正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神，长沙市举办了青少年机器人竞赛．组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共20个，若桌子腿数与凳子腿数的和为64条，则每个比赛场地有几张桌子和几条凳子？设有x张桌子，有y条凳子，根据题意所列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 64 \\ 4 x + 3 y = 20 \end{array}$ B、 ${\begin{array}{l} x + y = 20 \\ 4 x + 3 y = 64 \end{array}$ C、 ${\begin{array}{l} x + y = 64 \\ 3 x + 4 y = 20 \end{array}$ D、 ${\begin{array}{l} x + y = 20 \\ 3 x + 4 y = 64 \end{array}$

查看试题解析
7. 估计 $\sqrt{7}$ 的值在（）

A、4和5之间 B、3和4之间 C、2和3之间 D、1和2之间

查看试题解析
8. 如图，能推断 $A B / / C D$ 的是（）

A、∠2＝∠4 B、∠1＝∠5 C、∠3＝∠BAD D、∠B+∠BCD＝180°

查看试题解析
9. 已知点P（a，b），ab＞0，a＋b＜0，则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 口味虾、臭豆腐、嗦螺和糖油粑粑是是长沙著名的小吃，某兴趣小组在班级发动了一项“舌尖上的长沙-我最喜欢的长沙小吃”调查活动，发现结果满足以下三个条件：、
（1）喜欢嗦螺的人数少于喜欢口味虾的人数；
（2）喜欢嗦螺的人数多于喜欢臭豆腐的人数；
（3）喜欢臭豆腐的人数的3倍多于喜欢口味虾的人数．
若喜欢臭豆腐的人数为6，则喜欢嗦螺的人数的最大值为（）

A、16 B、6 C、17 D、7

查看试题解析

二、填空题

11. 比较大小： $\frac{\sqrt{2}}{2}$ $\frac{1}{2}$ （填写“＞”或“＜”或“＝”）.

查看试题解析
12. 点A（3，﹣4）到x轴的距离是

查看试题解析
13. 已知点M（m，m﹣1）在第四象限，则m的取值范围是．

查看试题解析
14. 已知关于 $x ， y$ 的二元一次方程组 ${\begin{array}{l} 2 x - y = 3 k + 2 \\ - x + 2 y = 4 \end{array}$ 的解满足 $x + y = 3$ ，则实数 $k$ 的值为．

查看试题解析
15. 将点P（2m+3，m﹣2）向上平移2个单位得到P′，且P′在x轴上，那么点P的坐标是．

查看试题解析
16. 如图，AB∥CD，CF平分∠DCG，GE平分∠CGB交FC的延长线于点E，若∠E＝34°，则∠B的度数为．

查看试题解析

三、解答题

17. 计算： $- 1^{2022} + | 1 - \sqrt{2} | - \sqrt[3]{8}$ ．

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} y = x - 4 \\ x + y = 6 \end{array}$

(2)、 ${\begin{array}{l} \frac{1}{2} x + y = 2 \\ x + 3 y = 5 \end{array}$

查看试题解析
19. 解不等式组 ${\begin{array}{l} x < \frac{x + 2}{3} \\ 2 (x + 2) \geq x + 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
20. 已知：如图，∠2＝∠C，∠1+∠EAB＝180°．

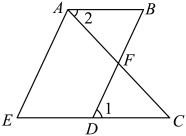(1)、求证：AE∥BD；

(2)、若∠1＝65°，∠2＝55°，求∠AFD的度数．

查看试题解析
21. 为了推动课堂教学改革，打造高效课堂，某中学对九年级部分学生就一学期以来线上教学方式的支持程度进行调查，下图为根据统计情况绘制的不完整统计图，请根据图中提供的信息，回答下列问题：

(1)、求本次被调查的九年级学生的人数；

(2)、通过计算补全条形统计图；

(3)、该校九年级学生共有540人，请你估计该校九年级有多少名学生支持线上教学方式（含“非常喜欢”和“喜欢”两种情况的学生）？

查看试题解析
22. 如图，在平面直角坐标系中，点A（ $a$ ， 0）为x轴上一点，点B（0，b）为y轴一点，其中 $a ， b$ 满足： $| a + 3 | + \sqrt{b - 4} = 0$ ．

(1)、求点A、B的坐标；

(2)、点C为y轴负半轴上一点，且△ABC的面积为12，求点C的坐标；

(3)、在（2）的条件下，在x轴上是否存在点P，使得△PBC的面积等于△ABC的面积的一半？若存在，求出相应的点P的坐标；若不存在，请说明理由．

查看试题解析
23. “中国人的饭碗必须牢牢掌握在咱们自己手中”．为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具．已知购进3件甲种农机具和2件乙种农机具共需4万元，购进1件甲种农机具和4件乙种农机具共需3万元．

(1)、求购进1件甲种农机具和1件乙种农机具各需多少万元？

(2)、若该粮食生产基地计划购进甲、乙两农机具共10件，且投入资金不少于9万元又不超过10万元，则有哪几种购买方案？

(3)、在（2）的条件下，哪种购买方案需要的资金最少，最少资金是多少？

查看试题解析
24. 如果一个一元一次方程的解在一个一元一次不等式（组）的解集范围内，则称该一元一次方程为该不等式（组）的关联方程．例：方程 $x - 1 = 0$ 是不等式 $x + 3 > 0$ 的关联方程．

(1)、试判断方程 $2 x + 3 = 1$ 是下列哪个不等式的关联方程① $2 - x < 0$ ； ② $3 (x + \frac{1}{6}) \geq \frac{5}{2}$ ；
③ $\frac{x - 1}{2} < 3$ ；请直接写出序号．

(2)、若关于 $x$ 的方程 $2 x - k = 1$ 是不等式组 ${\begin{array}{l} - (x - 1) > 3 \\ 2 x + 9 \geq 3 \end{array}$ 的关联方程，求 $k$ 的取值范围．

(3)、若方程 $3 - x = 2 x$ ， $3 + x = 2 (x + \frac{1}{2})$ 都是关于 $x$ 的不等式组 ${\begin{array}{l} x + 1 > m \\ x - m \leq 2 m + 1 \end{array}$ 的关联方程且不等式组的整数解有3个，求 $m$ 的取值范围．

查看试题解析
25. 如图所示，在平面直角坐标系中，如图①，将线段AB平移至线段CD，点A在x轴的负半轴，点C在y轴的正半轴上，连接AC、BD．

(1)、若A（﹣3，0）、B（﹣2，﹣2），C（0，2），直接写出点D的坐标；

(2)、如图②，在平面直角坐标系中，已知一定点M（2，0），两个动点E（a，2a+1）、F（b，﹣2b+3）．请你探索是否存在以两个动点E、F为端点的线段EF平行于线段OM且等于线段OM，若存在，求点E、F的坐标；若不存在，请说明理由；

(3)、如图③，在直线EF上有两点A、C，分别引两条射线AB、CD．∠BAF＝110°，∠DCF＝60°，射线AB、CD分别绕A点，C点以1度/秒和3度/秒的速度同时顺时针转动，设时间为t，在射线CD转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．

查看试题解析