广西壮族自治区南宁市2021-2022学年七年级下学期期末数学试卷

试卷更新日期：2022-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、-2 B、2 C、 $\frac{1}{2}$ D、 $\pm 2$

查看试题解析
2. “ $x$ 的2倍与3的和是非负数”列成不等式为（）

A、 $2 x + 3 \geq 0$ B、 $2 x + 3 > 0$ C、 $2 x + 3 \leq 0$ D、 $2 x + 3 < 0$

查看试题解析
3. 下列调查中，适合的是（）

A、调查南宁市人均每日废弃口罩的数量，采用全面调查方式 B、调查“嫦娥五号”月球探测器零件合格情况，采用抽样调查方式 C、为了精确调查你所在班级的同学的课外阅读时间，采用抽样调查方式 D、学校对学生进行体检，采用全面调查方式

查看试题解析
4. 如果 $a < b$ ，那么下列不等式正确的是（）

A、 $a + 1 > b + 1$ B、 $a - 1 > b - 1$ C、 $2 a < 2 b$ D、 $- 2 a < - 2 b$

查看试题解析
5. 如图，下列条件中，不能判断直线 $l_{1} / / l_{2}$ 的是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 = ∠ 3$ C、 $∠ 4 = ∠ 5$ D、 $∠ 2 + ∠ 4 = 180 °$

查看试题解析
6. 若4x^a+b－3y^a-b+2= 2是关于x，y的二元一次方程，则a+ b的值为（）

A、0 B、-1 C、1 D、2

查看试题解析
7. 某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见，随机对全校100名学生家长进行调查，这一问题中样本是（）

A、100 B、被抽取的100名学生家长 C、被抽取的100名学生家长的意见 D、全校学生家长的意见

查看试题解析
8. 点P在x轴上方，y轴左侧，距离x轴2个单位长度，距离y轴3个单位长度，则点P的坐标为（）

A、（2，3） B、（2，-3） C、（-3，-2） D、（-3，2）

查看试题解析
9. 我县某初中举行知识抢答赛，总共50道抢答题．抢答规定：抢答对1题得3分，抢答错1题扣1分，不抢答得0分．小军参加了抢答比赛，只抢答了其中的20道题，要使最后得分不少于50分，那么小军至少要答对（）

A、11题 B、15题 C、18题 D、20题

查看试题解析
10. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳六尺五寸；屈绳量之，不足二尺，木长几何？”意思是：用一根绳子去量一根木条，绳子还剩余6.5尺；将绳子对折再量木条，木条剩余2尺，问木条长多少尺？如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{array}{l} y = x + 6.5 \\ 0.5 y = x - 2 \end{array}$ B、 ${\begin{array}{l} y = x + 6.5 \\ y = 2 x - 1 \end{array}$ C、 ${\begin{array}{l} y = x - 6.5 \\ y = 2 x - 1 \end{array}$ D、 ${\begin{array}{l} y = x - 6.5 \\ 0.5 y = x + 2 \end{array}$

查看试题解析
11. 已知a，b两数在数轴上的位置如图所示，则化简代数式 $| b - a | - | 1 - a | - | b - 2 |$ 的结果是（）

A、1 B、2a﹣3 C、-1 D、2b﹣1

查看试题解析
12. 如图，已知GH//BC， $∠ 1 = ∠ 2$ ， $G F ⊥ A B$ ，给出下列结论：① $∠ B = ∠ A G H$ ；② $H E ⊥ A B$ ；③ $∠ D = ∠ F$ ；④HE平分∠AHG；其中正确的有（）

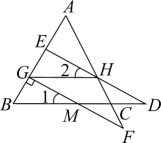A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 8的立方根为.

查看试题解析
14. 某校学生来自甲、乙、丙三个地区，其人数比为2：7：1，如图所示的扇形图表示上述分布情况．如果来自甲地区的为180人，则这个学校学生总数有人．

查看试题解析
15. 已知方程2x+y＝5，适用含x的代数式表示y，则y＝.

查看试题解析
16. 一大门的栏杆如图所示，BA垂直地面AE于点A，CD平行于地面AE，则∠ABC+∠BCD＝.

查看试题解析
17. 关于x的不等式组 ${\begin{array}{l} x - a < 0 \\ 2 x - 1 \geq 7 \end{array}$ 只有4个整数解，则a的取值范围是．

查看试题解析
18. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点A₁(0，1)，A₂(1，1)，A₃(1，0)，A₄(2，0)，…那么点A₂₀₂₂的坐标为.

查看试题解析

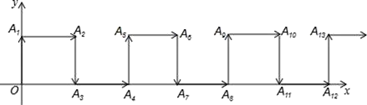
三、解答题

19. 计算： $\sqrt[3]{- 8} - | \sqrt{2} - 1 | + （ \sqrt{2} ）^{2} + \sqrt{25}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} 3 x - 9 < 0 \\ \frac{2 x - 4}{3} \leq x - 1 \end{array}$ 并将它们的解集在数轴上表示出来．

查看试题解析
21. 如图，三角形ABC三个顶点的坐标分别是A（3，4），B（-1，6），C（-2，-1），将三角形ABC向左平移5个单位长度，向下平移4个单位长度得到三角形A₁B₁C₁ ．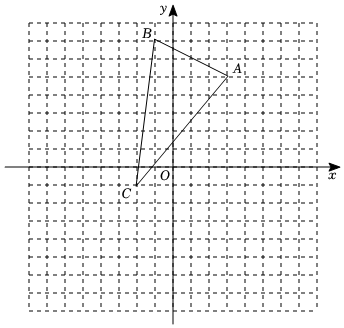

(1)、画出平移后的三角形A₁B₁C₁；

(2)、写出A₁、B₁、C₁的坐标；

(3)、求三角形A₁B₁C₁的面积．

查看试题解析
22. 阅读感悟：
已知实数x，y满足3x-y=5①，2x+3y=7②，求x-4y和7x+5y的值．
本题常规思路是将①②两式联立组成方程组，解得x，y的值再代人欲求值的式子中得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得式子的值，如由①－②可得x－4y=-2，由①+②×2可得7x+5y= 19．这样的解题思路就利用了通常所说的“整体思想”．

(1)、[解决问题]已知二元一次方程组 ${\begin{array}{l} x + 3 y = 6 \\ 3 x + y = 10 \end{array}$ ，则x-y= ， x+y=

(2)、[拓展延伸]某班级组织活动需购买小奖品，买18支铅笔、27本笔记本共需86.4元，买22支铅笔、13本笔记本共需53.6元，则购买5支铅笔、5本笔记本共需多少元？

查看试题解析
23. 暑假将至，某校组织学生进行“交通安全”知识竞赛，老师随机抽取了部分学生的成绩（得分取整数，满分100分），整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图．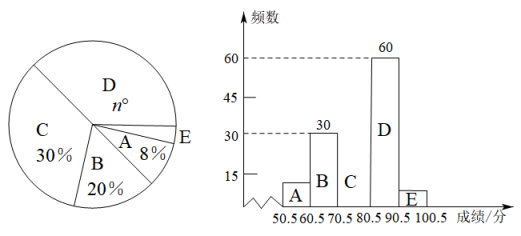
请根据以上信息，解答下列问题：

(1)、本次共抽取名学生成绩，A的频数值为，在扇形统计图中，n= ， E组所占比例为；

(2)、请补全频数分布直方图；

(3)、若全校共有1200名学生，根据抽样调查的结果，估计成绩在80分以上的学生人数有多少人？

查看试题解析
24. 某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求，决定增设篮球、足球两门选修课程，需要购进一批篮球和足球．已知购买2个篮球和3个足球共需费用510元；购买1个篮球和5个足球共需费用570元．

(1)、求篮球和足球的单价分别是多少元；

(2)、学校计划采购篮球和足球共50个，并要求篮球不少于30个，且总费用不超过5500元．那么有哪几种购买方案？

查看试题解析
25. 如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C＝∠EFG，∠CED＝∠GHD．

(1)、求证： $A B ∥ C D$ ；

(2)、若∠EHF＝70°，∠D＝50°，求∠AEM的度数．

查看试题解析
26. 如图①，在平面直角坐标系中，已知A（a，0），C（2，b），且满足 $| a + 3 | + \sqrt{b - 4} = 0$ ，过点C作BC⊥x轴于点B．

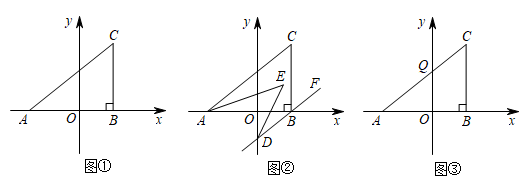(1)、填空：a= ， b＝；

(2)、如图②，过点B作BD//AC轴交y轴于点D，且AE，DE分别平分∠CAB，∠ODB，求∠AED的度数；

(3)、如图③，在y轴上是否存在点P，使得三角形ABP的面积与三角形ABC的面积相等？若存在，求出P的坐标；若不存在，请说明理由．

查看试题解析