四川省广安市岳池县2021-2022学年高一上学期数学期中考试试卷
试卷更新日期:2022-08-23 类型:期中考试
一、单选题
-
1. 已知集合A={-1,0,1,2,3}, , 则A∩B=( )A、{1} B、{0,1,2} C、{-1,3} D、{1,2,3}2. 若幂函数的图象经过点(2,),则其解析式为( )A、 B、 C、 D、3. 已知集合 ,映射 满足 的映射的个数共有( )个A、2 B、4 C、6 D、94. 下列函数中,是增函数的是( )A、f(x)= B、f(x)=()x C、f(x)=x2 D、f(x)=5. 已知函数 , 则的值是( )A、-1 B、3 C、 D、6. 下列函数中,既是偶函数又在区间上单调递减的是( )A、 B、 C、y=-x2+1 D、7. 函数f(x)=的定义域为( )A、[ , ) B、( , )∪( , +∞) C、(-2,) D、[-2,+∞)8. 某工厂产生的废气经过过滤后排放,规定排放时污染物的残留含量不得超过1%.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为:(为正常数,为原污染物数量).若前5个小时废气中的污染物被过滤掉了90%,那么要能够按规定排放废气,至少还需要过滤( )A、小时 B、小时 C、5小时 D、小时9. 在同一直角坐标系中,函数 且 的图象可能是( )A、
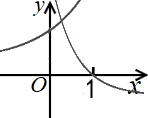 B、
B、 C、
C、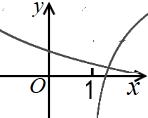 D、
D、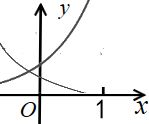 10. 已知函数f(x)=a-(a+1)x+1在区间(0,2)内单调递减,则实数a的取值范围是( )A、-1≤a≤ B、a≤ C、a≤-1 D、-1<a<11. 设函数是奇函数,在内是增函数,又 , 则的解集是( )A、或 B、或 C、或 D、或12. 若函数f(x)对任意实数x满足f(x+1)=-f(x),且当x∈(-1,0]时,有f(x)=-x,则函数y=f(x)的图象与y=log3|x|的图象的交点个数有( )A、1个 B、2个 C、3个 D、4个
10. 已知函数f(x)=a-(a+1)x+1在区间(0,2)内单调递减,则实数a的取值范围是( )A、-1≤a≤ B、a≤ C、a≤-1 D、-1<a<11. 设函数是奇函数,在内是增函数,又 , 则的解集是( )A、或 B、或 C、或 D、或12. 若函数f(x)对任意实数x满足f(x+1)=-f(x),且当x∈(-1,0]时,有f(x)=-x,则函数y=f(x)的图象与y=log3|x|的图象的交点个数有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知f(x+1)=x2+2x+4,则f(x)的最小值为.14. 已知 , , , 则a,b,c的大小关系是.(请用“<”连接)15. 设函数f(x)的定义域为R,f(x+1)为奇函数,f(x+2)为偶函数,当x∈[1,2]时,f(x)=ax2+b.若f(0)+f(3)=6,则f()=.16. 已知函数定义域为且满足 , 且时, , 若不等式f()≤f()+f(a)恒成立,则a∈.
三、解答题
-
17. 已知集合A={x|-2≤x≤4},集合B={x|m-1≤x≤2m+1}.(1)、当m=2时,求A∪B,;(2)、若A∪B=A,求实数m的取值范围.18. 计算下列各式的值:(1)、;(2)、.19. 已知函数(1)、画出函数的图象;(2)、若 , 求的取值范围.