江苏省南通市2022年中考数学试卷
试卷更新日期:2022-08-23 类型:中考真卷
一、选择题(本大题共10小题,每小题3分,共30分.)
-
1. 若气温零上记作 , 则气温零下记作( )A、 B、 C、 D、2. 下面由北京冬奥会比赛项目图标组成的四个图形中,可看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 沪渝蓉高铁是国家中长期铁路网规划“八纵八横”之沿江高铁通道的主通道,其中南通段总投资约39000000000元,将39000000000用科学记数法表示为( )A、 B、 C、 D、4. 用一根小木棒与两根长分别为的小木棒组成三角形,则这根小木棒的长度可以为( )A、 B、 C、 D、5. 如图是中5个相同的正方体搭成的立体图形,则它的主视图为( )
3. 沪渝蓉高铁是国家中长期铁路网规划“八纵八横”之沿江高铁通道的主通道,其中南通段总投资约39000000000元,将39000000000用科学记数法表示为( )A、 B、 C、 D、4. 用一根小木棒与两根长分别为的小木棒组成三角形,则这根小木棒的长度可以为( )A、 B、 C、 D、5. 如图是中5个相同的正方体搭成的立体图形,则它的主视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 李师傅家的超市今年1月盈利3000元,3月盈利3630元.若从1月到3月,每月盈利的平均增长率都相同,则这个平均增长率是( )A、10.5% B、10% C、20% D、21%7. 如图, , 则的度数是( )
6. 李师傅家的超市今年1月盈利3000元,3月盈利3630元.若从1月到3月,每月盈利的平均增长率都相同,则这个平均增长率是( )A、10.5% B、10% C、20% D、21%7. 如图, , 则的度数是( )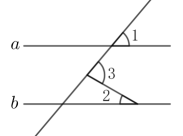 A、 B、 C、 D、8. 根据图像,可得关于x的不等式的解集是( )
A、 B、 C、 D、8. 根据图像,可得关于x的不等式的解集是( )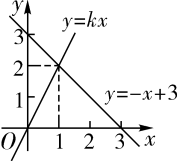 A、 B、 C、 D、9. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )
A、 B、 C、 D、9. 如图,在中,对角线相交于点O, , 若过点O且与边分别相交于点E,F,设 , 则y关于x的函数图象大致为( )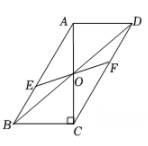 A、
A、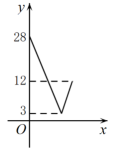 B、
B、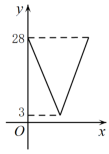 C、
C、 D、
D、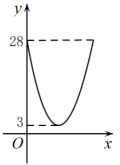 10. 已知实数m,n满足 , 则的最大值为( )A、24 B、 C、 D、-4
10. 已知实数m,n满足 , 则的最大值为( )A、24 B、 C、 D、-4二、填空题(本人题共8小题,第11~12题每小题3分,第13~18题每小题4分,共30分.)
-
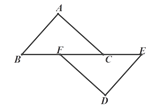
11. 为了了解“双减”背景下全国中小学生完成课后作业的时间情况,比较适合的调查方式是(填“全面调查”或“抽样调查”).12. 分式有意义,则x应满足的条件是 .13. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,余三.问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,多余3钱。问人数、羊价各是多少?若设人数为x,则可列方程为 .14. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,要使△ABC≌△DEF,还需添加一个条件是 . (只需添一个)
 15. 根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是 , 当飞行时间t为s时,小球达到最高点.16. 如图,B为地面上一点,测得B到树底部C的距离为 , 在B处放置高的测角仪 , 测得树顶A的仰角为 , 则树高为m(结果保留根号).
15. 根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是 , 当飞行时间t为s时,小球达到最高点.16. 如图,B为地面上一点,测得B到树底部C的距离为 , 在B处放置高的测角仪 , 测得树顶A的仰角为 , 则树高为m(结果保留根号). 17. 平面直角坐标系中,已知点是函数图象上的三点。若 , 则k的值为 .18. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .
17. 平面直角坐标系中,已知点是函数图象上的三点。若 , 则k的值为 .18. 如图,点O是正方形的中心, . 中,过点D,分别交于点G,M,连接 . 若 , 则的周长为 .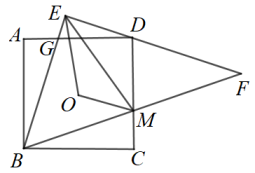
三、解答题(本大题共8小题,共90分.)
-
19.(1)、计算:;(2)、解不等式组:20. 为了了解八年级学生本学期参加社会实践活动的天数情况,A,B两个县区分别随机抽查了200名八年级学生.根据调查结果绘制了统计图表,部分图表如下:

A,B两个县区的统计表
平均数
众数
中位数
A县区
3.85
3
3
B县区
3.85
4
2.5
(1)、若A县区八年级共有约5000名学生,估计该县区八年级学生参加社会实践活动不少于3天的学生约为名;(2)、请对A,B两个县区八年级学生参加社会实践活动的天数情况进行比较,做出判断,并说明理由.21. 【阅读材料】老师的问题:
已知:如图, .
求作:菱形 , 使点C,D分别在上.
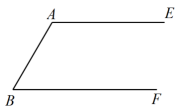
小明的作法:
(1)以A为圆心,长为半径画弧,交于点D;
(2)以B为圆心,长为半经画弧,交于点C;
(3)连接 .
四边形就是所求作的菱形,
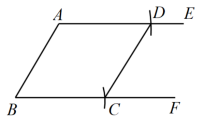
【解答问题】
请根据材料中的信息,证明四边形是菱形.
22. 不透明的袋子中装有红球、黄球、蓝球各一个,这些球除颜色外无其他差别.(1)、从袋子中随机摸出一个球,摸到蓝球的概率是;(2)、从袋子中随机摸出一个球后,放回并摇匀,再随机摸出一个球.求两次摸到的球的颜色为“一红一黄”的概率.23. 如图,四边形内接于 , 为的直径,平分 , 点E在的延长线上,连接 . (1)、求直径的长;(2)、若 , 计算图中阴影部分的面积.24. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
(1)、求直径的长;(2)、若 , 计算图中阴影部分的面积.24. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.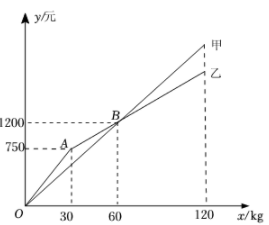 (1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.25. 如图,矩形中, , 点E在折线上运动,将绕点A顺时针旋转得到 , 旋转角等于 , 连接 .
(1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.25. 如图,矩形中, , 点E在折线上运动,将绕点A顺时针旋转得到 , 旋转角等于 , 连接 . (1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.26. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.(1)、在①;②;③三点中,是反比例函数图像的“1阶方点”的有(填序号);(2)、若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;(3)、若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.
(1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.26. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.(1)、在①;②;③三点中,是反比例函数图像的“1阶方点”的有(填序号);(2)、若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;(3)、若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.