四川省绵阳市江油市2021-2022学年七年级下学期期中数学试卷
试卷更新日期:2022-08-23 类型:期中考试
一、单选题
-
1. 在 , ,0, 这四个数中,为无理数的是 ( )A、 B、 C、0 D、2. 9的算术平方根是( )A、 ﹣3 B、±3 C、3 D、3. 如图,直线AB、CD相交于O,OA平分∠EOC,若 , 那么∠BOD的度数是( )
 A、 B、 C、 D、4. 如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( )
A、 B、 C、 D、4. 如图,工人师傅用角尺画出工件边缘AB的垂线a和b,得到a∥b,理由是( )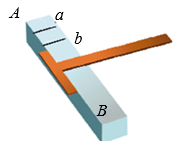 A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行5. 两个直角三角板如图摆放,其中 , , , AB与DF交于点M.若 , 则的大小为( )
A、连结直线外一点与直线上各点的所有线段中,垂线段最短 B、在同一平面内,垂直于同一条直线的两条直线互相平行 C、在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线 D、经过直线外一点,有且只有一条直线与这条直线平行5. 两个直角三角板如图摆放,其中 , , , AB与DF交于点M.若 , 则的大小为( ) A、 B、 C、 D、6. 如果一个数的立方根等于这个数本身,那么这个数是( )A、0,1 B、1, C、0, D、0,7. 如图,三角形AOB中, , , 则△AOB的面积为( )
A、 B、 C、 D、6. 如果一个数的立方根等于这个数本身,那么这个数是( )A、0,1 B、1, C、0, D、0,7. 如图,三角形AOB中, , , 则△AOB的面积为( ) A、14 B、12 C、10 D、158. 若 , 则与的关系一定是( )A、 B、 C、 D、9. 无理数在数轴上位置的描述,正确的是( )A、在点的左边 B、在点的右边 C、和原点的距离小于3 D、和原点的距离大于310. 将点向右平移4个单位,向上平移2个单位,得到点P的对应点的坐标是( )A、 B、 C、 D、11. 若规定表示不超过a的最大整数,例如 , , 若 , , 则在此规定下的值为( )A、0 B、1 C、 D、12. 如图,已知直线 , 则∠α、∠β、∠γ之间的关系是( )
A、14 B、12 C、10 D、158. 若 , 则与的关系一定是( )A、 B、 C、 D、9. 无理数在数轴上位置的描述,正确的是( )A、在点的左边 B、在点的右边 C、和原点的距离小于3 D、和原点的距离大于310. 将点向右平移4个单位,向上平移2个单位,得到点P的对应点的坐标是( )A、 B、 C、 D、11. 若规定表示不超过a的最大整数,例如 , , 若 , , 则在此规定下的值为( )A、0 B、1 C、 D、12. 如图,已知直线 , 则∠α、∠β、∠γ之间的关系是( )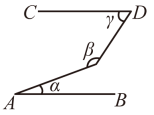 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 电影票上“6排8号”,记作 , 则“2排3号”记作 .14. 把命题“二直线平行,内错角相等”改写成“如果 , 那么”的形式.15. 已知 , x是整数,则x的最小值是 .16. 若点M在第二象限,且点M到x轴的距离为2,到y轴的距离为1,则点M的坐标为 .17. 若的整数部分为a,小数部分为b,则的值为 .18. 某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中, , ;图②中, , .图③是该同学所做的一个实验:他将 的直角边 与 的斜边 重合在一起,并将 沿 方向移动.在移动过程中, 、 两点始终在 边上(移动开始时点 与点 重合).要使 、 的连线与 平行,此时 的度数为.

三、解答题
-
19.(1)、解方程:(2)、解方程:20.(1)、计算:(2)、如图所示的是某学校的平面示意图,已知旗杆的位置是 , 实验室的位置是 .

①根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂,宿舍楼和大门的位置.
②已知办公楼的位置是 , 教学楼的位置是 , 在①中所画的图中标出办公楼和教学楼的位置.
21. 在平面直角坐标系中,点A的坐标为(3,2).请标出点A,并回答下列问题:
( 1 )作AM⊥x轴于M,并延长AM至点B,使BM=AM,直接写出点B的坐标;
( 2 )作AN⊥y轴于N,并延长AN至点D,使DN=AN,直接写出点D的坐标;
( 3 )连接AO并延长至点C,使得CO=AO,直接写出点C的坐标;
( 4 )直接说出四边形ABCD的形状.(不需要证明)
22. 如图, , .求证: . 请完成证明过程.

证明:
∵ , (已知)
∴ ( )
又∵ , (已知)
∴ , (等量代换)
∴ ,( )
∴ . ( )


