江苏省扬州市江都区八校2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 北京 2022年冬奥会会徽是以汉字“冬”为灵感来源设计的.在下面如图的四个图中，由如图经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $a^{5} + a^{5} = a^{10}$ B、 $a^{5} \times a^{6} = a^{30}$ C、 $a^{6} \div a^{5} = a$ D、 $a^{4} \div a^{4} = 0$

查看试题解析
3. 如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（）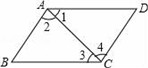

A、∠1＝∠3 B、∠B＋∠BCD＝180° C、∠2＝∠4 D、∠D＋∠BAD＝180°

查看试题解析
4. 下列左边到右边的变形，属于因式分解的是（）

A、 $x^{2} - 1 = (x + 1) (x - 1)$ B、 $x^{2} + 1 = x (x + \frac{1}{x})$ C、 $(a + 1) (a - 1) = a^{2} - 1$ D、 $x^{2} - 16 + 3 x = (x^{} + 4) (x - 4) + 3 x$

查看试题解析
5. 已知一个三角形的两边长分别是2和7，第三边为偶数，则此三角形的周长是（）

A、15 B、16 C、17 D、15或17

查看试题解析
6. 已知 $a = (- 0.2)^{0}$ ， $b = - 2^{- 1}$ ， $c = {(- \frac{1}{2})}^{- 2}$ ，比较 $a$ ， $b$ ， $c$ 的大小（）

A、 $a < b < c$ B、 $b < c < a$ C、 $a < c < b$ D、 $b < a < c$

查看试题解析
7. 如图，将三角形纸片ABC沿DE折叠，当点A落在四边形BCDE的外部时，测量得∠1＝70°，∠2＝152°，则∠A为（）

A、40° B、42° C、30° D、52°

查看试题解析
8. 为了书写简便，数学家欧拉引进了求和符号“ $\sum$ ”．如记 $\sum_{k = 1}^{n} k = 1 + 2 + 3 + ... + (n - 1) + n MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaaqahabaGaam4Aaiab
g2da9iaaigdacqGHRaWkcaaIYaGaey4kaSIaaG4maiabgUcaRiaac6
cacaGGUaGaaiOlaiabgUcaRmaabmaapaqaa8qacaWGUbGaeyOeI0Ia
aGymaaGaayjkaiaawMcaaiabgUcaRiaad6gaaSqaaiaadUgacqGH9a
qpcaaIXaaabaGaaeOBaaqdcqGHris5aaaa@5506@$ ， $\sum_{k = 3}^{n} (x + k) = (x + 3) + (x + 4) + ... + (x + n) MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaaqahabaWaaeWaa8aa
baWdbiaadIhacqGHRaWkcaWGRbaacaGLOaGaayzkaaGaeyypa0Zaae
Waa8aabaWdbiaadIhacqGHRaWkcaaIZaaacaGLOaGaayzkaaGaey4k
aSYaaeWaa8aabaWdbiaadIhacqGHRaWkcaaI0aaacaGLOaGaayzkaa
Gaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSYaaeWaa8aabaWdbiaa
dIhacqGHRaWkcaWGUbaacaGLOaGaayzkaaaaleaacaWGRbGaeyypa0
JaaG4maaqaaiaad6gaa0GaeyyeIuoaaaa@5C66@$ ，已知 $\sum_{k = 2}^{n} [(x + k) (x - k + 1)] = 4 x^{2} + 4 x + m MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbWexLMBbXgBd9gzLbvyNv2CaeHbl7mZLdGeaGqiVu0Je9sqqr
pepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs
0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaai
aabeqaamaabaabauaakeaaqaaaaaaaaaWdbmaawahabeWcpaqaa8qa
caWGRbGaeyypa0JaaGOmaaWdaeaapeGaamOBaaqdpaqaa8qacqGHri
s5aaGcdaWadaWdaeaapeWaaeWaa8aabaWdbiaadIhacqGHRaWkcaWG
RbaacaGLOaGaayzkaaWaaeWaa8aabaWdbiaadIhacqGHsislcaWGRb
Gaey4kaSIaaGymaaGaayjkaiaawMcaaaGaay5waiaaw2faaiabg2da
9iaaisdacaWG4bWdamaaCaaaleqabaWdbiaaikdaaaGccqGHRaWkca
aI0aGaamiEaiabgUcaRiaad2gaaaa@5A83@$ ，则m的值是（）

A、-50 B、-70 C、-40 D、-20

查看试题解析

二、填空题

9. 某种新型冠状病毒的大小约为125纳米，即0.000000125米，用科学记数法表示这个数为．

查看试题解析
10. 计算： ${(- 2 a^{2})}^{3} =$ ．

查看试题解析
11. 一个等腰三角形的两边长分别为4cm和9cm，则它的周长为cm.

查看试题解析
12. 已知 $a - 2 b = 2$ ，则 $2^{a} \div 4^{b}$ 的值是．

查看试题解析
13. 学校准备组织花样跑操比赛，体育委员李明设置的跑操线路如图所示，从A点出发沿直线前进10米到达B点后向左旋转α度，再沿直线前进10米，到达点C后，又向左旋转相同的角度，照这样走下去，他第一次回到出发地点时，共走了100米，则他每次旋转的角度α为度．

查看试题解析
14. 如果 $(x + 1) (x^{2} - 4 a x + a)$ 的乘积中不含 $x^{2}$ 项，则a为．

查看试题解析
15. 若 $x^{2} - (m - 4) x + 25$ 是完全平方式，则 $m$ 的值为．

查看试题解析
16. 如图，将一个长方形纸条折成如图的形状，若已知∠2＝55°，则∠1＝°.

查看试题解析
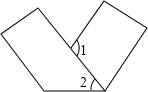17. 若2a－3b=－1，则代数式4a²－6ab+3b的值为．

查看试题解析
18. 如图，AB⊥BC，AE平分∠BAD交BC于点E，AE⊥DE，∠1+∠2＝90°，M、N分别是BA，CD延长线上的点，∠EAM和∠EDN的平分线交于点F．下列结论：①AB∥CD；②∠AEB+∠ADC＝180°；③DE平分∠ADC；④∠F为定值．其中结论正确的有．

查看试题解析

三、解答题

19. 计算：

(1)、 $- 1^{2007} + {(π - 3)}^{0} - {(- \frac{1}{2})}^{- 2}$

(2)、 ${(a + 2 b)}^{2} - (a + b) (a - 2 b)$

查看试题解析
20. 因式分解

(1)、 $a b^{2} - 4 a$

(2)、 $x^{4} - 8 x^{2} y^{2} + 16 y^{4}$

查看试题解析
21. 解方程组

(1)、 ${\begin{array}{l} y = 2 x \\ 7 x + y = 9 \end{array}$

(2)、 ${\begin{array}{l} 3 x + 4 y = 4 \\ x - 2 y = 3 \end{array}$

查看试题解析
22. 先化简，再求值： ${(2 x + 3 y)}^{2} + 3 x (x + 3 y) - (2 x + y) (2 x - y)$ ，其中x=1，y=-2

查看试题解析
23. 如图，在方格纸内将△ABC水平向右平移4个单位得到△A'B'C'．

(1)、补全△A'B'C'，利用网格点和直尺画图；

(2)、图中AC与A'C'的关系是：；

(3)、画出△ABC中AB边上的中线CD与高CE；

(4)、平移过程中，线段AC扫过的面积是．

查看试题解析
24. 已知：如图，∠BAE+∠AED=180°，∠1=∠2，∠M和∠N有怎样的数量关系，并说明理由．

查看试题解析
25. 如图，∠1＝∠BCE，∠2+∠3＝180°．

(1)、判断AC与EF的位置关系，并说明理由；

(2)、若CA平分∠BCE，EF⊥AB于F，∠1＝72°，求∠BAD的度数．

查看试题解析
26. 已知 $m - n = 4 ， m n = - 3$

(1)、计算： $m^{2} + n^{2}$

(2)、求 $(m^{2} - 4) (n^{2} - 4 ）$ 的值；

(3)、求 $8^{m} \cdot 3 2^{n} \div 4^{m + 2 n}$ 的值．

查看试题解析
27. 阅读下列材料：若一个正整数 $x$ 能表示成 $a^{2} - b^{2}$ （a，b是正整数， $a > b$ ）的形式，则称这个数为“明礼崇德数”，a与b是x的一个平方差分解，例如 $5 = 3^{2} - 2^{2}$ ，所以 $5$ 是“明礼崇德数” $3$ 与 $2$ 是 $5$ 的平方差分解；再如： $M = x^{2} + 2 x y = x^{2} + 2 x y + y^{2} - y^{2} = {(x + y)}^{2} - y^{2}$ （ $x ， y$ 为正整数），所以 $M$ 也是“明礼崇德数”，（ $x + y$ ）与 $y$ 是 $M$ 的一个平方差分解．

(1)、判断 $9$ “明礼崇德数”（填“是”或“不是”）；

(2)、已知 $(x^{2} + y)$ 与 $x^{2}$ 是 $P$ 的一个平方差分解，求代数式P；

(3)、已知 $N = 2 x^{2} - 3 y^{2} + 8 x - 18 y + k$ （ $x ， y$ 是正整数， $k$ 是常数，且 $x > y + 1$ ），要使 $N$ 是“明礼崇德数”，试求出符合条件的 $k$ 值，并说明理由．

查看试题解析
28. 已知 $△ A B C$ ， $∠ A B C = 80 °$ ，点 $E$ 在 $B C$ 边上，点 $D$ 是射线 $A B$ 上的一个动点，将 $△ A B D$ 沿 $D E$ 折叠，使点 $B$ 落在点 $B^{'}$ 处，

(1)、如图 $1$ ，若 $∠ A D B^{'} = 125 °$ ，求 $∠ C E B^{'}$ 的度数；

(2)、如图 $2$ ，试探究 $∠ A D B^{'}$ 与 $∠ C E B^{'}$ 的数量关系，并说明理由；

(3)、连接 $C B^{'}$ ，当 $C B^{'} / / A B$ 时，直接写出 $∠ C B^{'} E$ 与 $∠ A D B^{'}$ 的数量关系为．

查看试题解析