江苏省扬州市邗江区2021-2022学年七年级下学期期中考试数学试卷

试卷更新日期：2022-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，不能通过其中一个四边形平移得到的是（）

A、 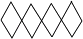B、 C、 D、

查看试题解析
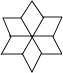2. 如图，给出了过直线外一点作已知直线的平行线的方法，其依据是（）

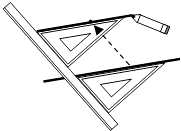A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、两直线平行，同位角相等

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} + a^{4} = a^{6}$ B、 $(- a)^{2} \cdot a^{3} = a^{5}$ C、 $(a^{2})^{2} = a^{5}$ D、 $(a - b)^{2} = a^{2} - b^{2}$

查看试题解析
4. 下列给出的各组线段的长度中，能组成三角形的是（）

A、3，4，9 B、6，8，15 C、5，7，12 D、4，7，10

查看试题解析
5. 如图，下列条件中：① $∠ B + ∠ B A D = 180 °$ ；② $∠ B = ∠ 5$ ；③ $∠ 3 = ∠ 4$ ；④ $∠ 1 = ∠ 2$ ；能判定 $A D ∥ B C$ 的条件个数有（）

A、1 B、2 C、3 D、4

查看试题解析
6. 若∠1与∠2的关系是同位角，∠1=30°，则∠2=（）

A、30° B、150° C、50°或130° D、不确定

查看试题解析
7. 如图，∠ABD、∠ACD的角平分线交于点P，若∠A = 50°，∠D =10°，则∠P的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
8. 现有一张边长为 $a$ 的大正方形卡片和三张边长为 $b$ 的小正方形卡片 $(\frac{1}{2} a < b < a)$ 如图 $1$ ，取出两张小正方形卡片放入“大正方形卡片”内拼成的图案如图 $2$ ，再重新用三张小正方形卡片放入“大正方形卡片”内拼成的图案如图 $3$ ，已知图 $3$ 中的阴影部分的面积比图 $2$ 中的阴影部分的面积大 $2 a b - 15$ ，则小正方形卡片的面积是（）

A、 $10$ B、 $8$ C、 $2$ D、 $5$

查看试题解析

二、填空题

9. 流感病毒的半径约为0.000000045m，用科学记数法表示为m

查看试题解析
10. 一个多边形的每一个外角都等于18°，它是边形．

查看试题解析
11. 计算 ${(\frac{2}{3})}^{2019} \times (- 1.5)^{2020}$ 的结果是．

查看试题解析
12. 已知 $(x + 4) (x - 9) = x^{2} + m x - 36$ ，则 $m$ 的值为．

查看试题解析
13. 若 $4 x^{2} + k x + 9$ 是一个完全平方式，则 $k$ 的值是．

查看试题解析
14. 已知 $a = 2^{33}$ ， $b = 3^{22}$ 则 $a$ $b$ （填“ $＞$ ”、“ $＜$ ”或“ $=$ ”）

查看试题解析
15. 若 $| a - b | = 3$ ，则 $b^{2} - 2 a b + a^{2}$ 的值为．

查看试题解析
16. 如图，把矩形 $A B C D$ 沿 $E F$ 折叠，若 $∠ 1 = 40 °$ ，则 $∠ A E F =$ °．

查看试题解析
17. 如图是一副形似“秋蝉”的图案，实线部分是由正方形、正五边形和正六边形叠放在一起形成的，则图中∠MON的度数为°．

查看试题解析
18. 已知（2016-a+b-c）（2017-a+b-c）=6，则 $(2016 - a + b - c)^{2} + (2017 - a + b - c)^{2}$ 的值是．

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- \frac{1}{3})}^{- 2} + {(\frac{1}{9})}^{0} + {(- 5)}^{3} \div {(- 5)}^{2}$

(2)、 ${(2 x - y)}^{2} - (x - y) (y + x)$

查看试题解析
20. 因式分解

(1)、 $m^{2} - 10 m ＋ 25$

(2)、 $(x^{2} + 4 y^{2})^{2} - 16 x^{2} y^{2}$

查看试题解析
21. 有这样一道题：计算（2x﹣3）（3x+1）﹣6x（x+3）+25x+15的值，其中x=2018．小刚把x=2018错抄成x=2081，但他的计算结果也是正确的，请通过计算说明原因．

查看试题解析
22. 如图，在△ABC中，∠B＝36°，∠C＝76°，AD是△ABC的角平分线，BE是△ABD中AD边上的高，求∠ABE的度数．

查看试题解析
23. 画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸中将△ABC经过一次平移后得到△A′B′C′，图中标出了点C的对应点C′．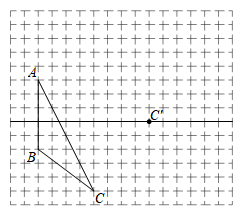

(1)、请画出平移后的△A′B′C′；

(2)、若连接AA′，BB′，则这两条线段之间的关系是；

(3)、利用网格画出△ABC中AC边上的中线BD；

(4)、在平移过程中，线段AB扫过的面积为．

查看试题解析
24. 在△ABC中，∠1=∠2，∠3=∠4，∠BAC=54°，求∠DAC的度数.

查看试题解析
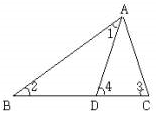25. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．

(1)、CD与EF平行吗？请说明理由；

(2)、如果∠1＝∠2，且∠3＝110°，求∠ACB的度数．

查看试题解析
26. 图a是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图b的形状拼成一个正方形．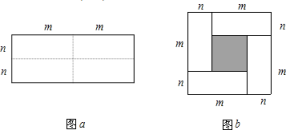

(1)、请用两种不同的方法，求图b中阴影部分的面积：
方法1：；方法2：；

(2)、观察图b，写出代数式 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $m n$ 之间的等量关系，并通过计算验证；

(3)、根据（2）题中的等量关系，解决如下问题：若 $2 a + b = 7$ ， $a b = 3$ ，求 $(2 a - b)^{2}$ 的值．

查看试题解析
27. 对于形如x²+2ax+a²这样的二次三项式，可以用公式法将它分解成（x+a）²的形式．但对于二次三项式x²+2ax-3a² ，就不能直接运用公式了．此时，我们可以在二次三项式x²+2ax-3a²中先加上一项a² ，使它与x²+2ax的和成为一个完全平方式，再减去a² ，整个式子的值不变，于是有：x²+2ax-3a²= x²+2ax+a²- a²- 3a²=（x+a）²- （2a）²=（x+3a）（x -a），像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”．

(1)、利用“配方法”分解因式：
①x²-8x-9
② a⁴+a²b²+ b⁴

(2)、若a+ b=4，ab=2，求①a²+b²；②a⁴+b⁴的值.

(3)、已知x是任意实数，试比较 $x^{2} - 4 x + 5$ 与 $- x^{2} + 4 x - 4$ 的大小，说明理由．

查看试题解析
28. 我们知道：光线反射时，反射光线、入射光线和法线在同一平面内，反射光线、入射光线分别在法线两侧，反射角等于入射角．
如图1，EF为一镜面，AO为入射光线，入射点为点O，ON为法线（过入射点O且垂直于镜面EF的直线），OB为反射光线，此时反射角∠BON等于入射角∠AON．

(1)、如图1，若∠AOE=65°，则∠BOF=°；若∠AOB=80°，则∠BOF= °；

(2)、两平面镜OP、OQ相交于点O，一束光线从点A出发，经过平面镜两次反射后，恰好经过点B．
①如图2，当∠POQ为多少度时，光线 $A M ∥ N B$ ？请说明理由．
②如图3，若两条光线AM、NB相交于点E，请探究∠POQ与∠MEN之间满足的等量关系，并说明理由．
③如图4，若两条光线AM、NB所在的直线相交于点E，∠POQ与∠MEN之间满足的等量关系是 ▲ （直接写出结果）

查看试题解析