江苏省扬州市广陵区2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 计算（﹣x³）²的结果是（）

A、x⁵ B、x⁶ C、﹣x⁵ D、﹣x⁶

查看试题解析
2. 若a+b=1，则a²﹣b²+2b的值为（）

A、4 B、3 C、1 D、0

查看试题解析
3. 若a=（﹣ $\frac{3}{2}$ ）^﹣² ， b=（﹣1）^﹣¹ ， c=（﹣ $\frac{π}{2}$ ）⁰ ，则a，b，c的大小关系是（）

A、a＞b＞c B、a＞c＞b C、c＞a＞b D、c＞b＞a

查看试题解析
4. 英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯，荣获了诺贝尔物理学奖，石墨烯的理论厚度仅0.000 000 000 34米，将这个数用科学记数法表示为（）

A、0.34×10^－9 B、3.4×10^－9 C、3.4×10^－10 D、3.4×10^－11

查看试题解析
5. 如图，已知a∥b，∠1＝75°，则∠2的度数是（）

A、35° B、75° C、105° D、125°

查看试题解析
6.
已知直线a∥b ，将一副三角板按如图所示放置在两条平行线之间，则∠1的度数是

A、45° B、60° C、75° D、80°

查看试题解析
7. 如图，直线m∥n，△ABC的顶点B，C分别在直线n，m上，且∠ACB=90°，若∠1=40°，则∠2的度数为（）

A、140° B、130° C、120° D、110°

查看试题解析
8. 如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K﹣∠H=27°，则∠K=（）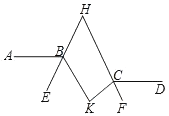

A、76° B、78° C、80° D、82°

查看试题解析

二、填空题

9. ﹣21a²b³c÷3ab= ．

查看试题解析
10. 如图，AB∥CD，点P为CD上一点，∠EBA、∠EPC的角平分线于点F，已知∠F＝40°，则∠E＝度.

查看试题解析
11. 如图，把一张长方形的纸条ABCD沿EF折叠，若∠BFC′比∠BFE多6°，则∠EFC= ．

查看试题解析
12. 若代数式x²+（m+1）x+1是一个完全平方式，则常数m的值为

查看试题解析
13. 一个多边形的每一个内角为150°，那么这个多边形的边数为．

查看试题解析
14. 如果10^m=12，10ⁿ=3，那么10^m+n=.

查看试题解析
15. 已知a²-b²=12，a﹣b=2，则a+b= ．

查看试题解析
16. 代数式3x²﹣4x+6的值为9，则x²﹣ $\frac{4}{3} x$ +6的值为

查看试题解析
17. 如图，有三种卡片，其中边长为a的正方形卡片1张，边长分别为a、b的矩形卡片6张，边长为b的正方形卡片9张．用这16张卡片拼成一个正方形，则这个正方形的边长为．

查看试题解析
18. 如图，△ABC中，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC＝120°，∠BGC＝102°，则∠A的度数为

查看试题解析

三、解答题

19. 计算

(1)、3x³•x⁹﹣2x•x³•x⁸

(2)、（2﹣π）⁰+（ $\frac{1}{2}$ ）^﹣²+（﹣2）³

(3)、（x+4）（x﹣4）﹣（x﹣2）²

(4)、（x+2）（x﹣3）﹣x（x+1）

查看试题解析
20. 把下列各式分解因式

(1)、16ab²﹣48a²b

(2)、2m³-18m

(3)、（x²+4）²﹣16x²

查看试题解析
21. 已知x+y＝4，xy＝1，求下列各式的值：

(1)、x²y+xy²；

(2)、（x²﹣1）（y²﹣1）.

查看试题解析
22.
在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移后得△DEF，使点A的对应点为点D，点B的对应点为点E．

(1)、画出△DEF；

(2)、连接AD、BE，则线段AD与BE的关系是；

(3)、求△DEF的面积．

查看试题解析
23. 如图，一块平面反光镜在∠AOB的边OA上，∠AOB=40°，在OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，由科学实验知道：∠OQP=∠AQR，求∠QPB的度数．

查看试题解析
24. 如图，大小两个正方形边长分别为a、b．

(1)、用含a、b的代数式阴影部分的面积S；

(2)、如果a+b=7，ab=5，求阴影部分的面积．

查看试题解析
25. 如图，AB//CD，AE平分∠BAD，CD与AE相交于F，∠CFE＝∠E．求证：AD//BC．

查看试题解析
26. 阅读材料：若m²﹣2mn+2n²﹣8n+16=0，求m、n的值．
解：∵m²﹣2mn+2n²﹣8n+16=0，∴（m²﹣2mn+n²）+（n²﹣8n+16）=0∴（m﹣n）²+（n﹣4）²=0，∴（m﹣n）²=0，（n﹣4）²=0，∴n=4，m=4．
根据你的观察，探究下面的问题：

(1)、a²+b²﹣2a+1=0，则a= ． b= ．

(2)、已知x²+2y²﹣2xy+6y+9=0，求xy的值．

(3)、△ABC的三边长a、b、c都是正整数，满足2a²+b²﹣4a﹣6b+11=0，求△ABC的周长．

查看试题解析
27.

(1)、光线从空气中射入水中会产生折射现象，同时光线从水中射入空气中也会产生折射现象，如图1，光线a从空气中射入水中，再从水中射入空气中，形成光线b，根据光学知识有∠1＝∠2，∠3＝∠4，请判断光线a与光线b是否平行，并说明理由；

(2)、如图2，直线EF上有两点A、C，分别引两条射线AB、CD．已知∠BAF＝150°，∠DCF＝80°，射线AB、CD分别绕点A、点C以1度/秒和3度/秒的速度同时顺时针转动，设时间为t秒，当射线CD转动一周时，两条射线同时停止．则当直线CD与直线AB互相垂直时，t＝秒．

查看试题解析
28. 已知，AB∥CD，点E为射线FG上一点．

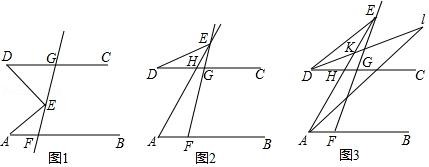(1)、如图1，若∠EAF=30°，∠EDG=40°，则∠AED=°；

(2)、如图2，当点E在FG延长线上时，此时CD与AE交于点H，则∠AED、∠EAF、∠EDG之间满足怎样的关系，请说明你的结论；

(3)、如图3，DI平分∠EDC，交AE于点K，交AI于点I，且∠EAI：∠BAI=1：2，∠AED=22°，∠I=20°，求∠EKD的度数．

查看试题解析