江苏省盐城市大丰区2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，可以由其中一个图形通过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 以下列各组线段的长为边，能组成三角形的是（）

A、2、4、7 B、3、5、2 C、7、7、3 D、9、5、3

查看试题解析
3. 下列各式运算正确的是（）．

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $a^{5} \div a^{3} = a^{2}$

查看试题解析
4. 如图，下列条件能判断AB∥CD的是（）

A、∠1＝∠3 B、∠2＝∠3 C、∠1＝∠4 D、∠2＝∠4

查看试题解析
5. 下列各式从左边到右边的变形是因式分解的是（）

A、 $(a - 1) (a + 2) = a^{2} + a - 2$ B、 $(a + 2) (a - 2) = a^{2} - 4$ C、 $a^{2} + 2 a + 1 = a (a + 2) + 1$ D、 $a^{2} - 4 a + 4 = {(a - 2)}^{2}$

查看试题解析
6. 若一个凸多边形的内角和为720°，则这个多边形的边数为 $($ 　　 $)$

A、4 B、5 C、6 D、7

查看试题解析
7. 若（x+2）（2x﹣n）＝2x²+mx﹣2，则m+n＝（）

A、4 B、6 C、2 D、﹣4

查看试题解析
8. 如图，若AB∥CD ，则∠A、∠E、∠D之间的是（）

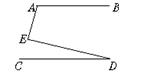A、∠A+∠E+∠D=180° B、∠A+∠E－∠D=180° C、∠A－∠E+∠D=180° D、∠A+∠E+∠D=270°

查看试题解析

二、填空题

9. 计算： $a^{2} \cdot a =$ ．

查看试题解析
10. 熔喷布，俗称口罩的“心脏”，是口罩中间的过滤层，能过滤细菌，阻止病菌传播.经测量，医用外科口罩的熔喷布厚度约为0.000156米，将0.000156用科学记数法表示应为.

查看试题解析
11. 分解因式：x²-2x+1=.

查看试题解析
12. 计算： ${(- \frac{1}{3})}^{2021} \times 3^{2022} =$ ．

查看试题解析
13. 如图，将三角板的直角顶点放在直尺的一边上，若∠1=65°，则∠2的度数为.

查看试题解析
14. 若 $x^{2} + m x + 9$ 是关于 $x$ 的完全平方式，则m的值是．

查看试题解析
15. 如图，∠1、∠2、∠3、∠4是五边形的外角，若∠A＝120°，则∠1+∠2+∠3+∠4＝．

查看试题解析
16. 如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依次为2、3、4、6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任两个螺丝间的距离的最大值为．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(π - 3.14)}^{0} + {(- \frac{1}{2})}^{- 2}$ ；

(2)、 $m (m + 5) - (m - 3) (m + 2)$ ．

查看试题解析
18. 因式分解：

(1)、 $4 a^{2} + 4 a + 1$ ；

(2)、 $4 x^{2} - 16$ ．

查看试题解析
19. 先化简，再求值： $4 {(x - 2)}^{2} - (2 x + 3) (2 x - 3)$ ，其中 $x = - 1$ ．

查看试题解析
20. 在如图所示的正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的顶点都在正方形网格的格点上．

(1)、画出△ABC先向右平移5个单位长度，再向上平移2个单位长度所得的△A₁B₁C₁；

(2)、画出△ABC的中线AD；

(3)、画出△ABC中AC边上的高BE；（要求只能通过连接格点方式作图）

(4)、计算△ABC的面积为．

查看试题解析
21. 完成下面的证明过程．
已知：如图，点E、F分别在AB、CD上，AD分别交EC、BF于点H、G，∠1＝∠2，∠B＝∠C．求证∠A＝∠D．

证明：∵∠1＝∠2（已知），

∠2＝∠AGB（   ），

∴∠1＝    ．

∴EC∥BF（    ）．

∴∠B＝∠AEC（          ）．

又∵∠B＝∠C（已知），

∴∠AEC＝．

∴ （    ）．

∴∠A＝∠D（    ）．

查看试题解析
22. 已知 $2^{m} = 5$ ， $2^{n} = 3$ ，求下列各式的值：

(1)、 $2^{m + n}$ ；

(2)、 $4^{m} \times 8^{n}$ ；

(3)、 $2^{m - 2 n}$ ．

查看试题解析
23. 如图，D、E、F分别在△ABC的三条边上，DE∥AB，∠1+∠2=180°．

(1)、试说明：DF∥AC；

(2)、若∠1=110°，DF平分∠BDE，求∠C的度数．

查看试题解析
24. 已知下列等式：
① $3^{2} - 1^{2} = 8$

② $5^{2} - 3^{2} = 16$

③ $7^{2} - 5^{2} = 24$

……

(1)、请仔细观察，写出第5个式子；

(2)、根据以上式子的规律，写出第n个式子，并用所学知识说明第n个等式成立；

(3)、利用发现的规律计算：8+16+24+……+392+400．

查看试题解析
25. 如图，在四边形ABCD中，∠A＝140°，∠D＝80°．

(1)、如图1，若∠B＝∠C，则∠C＝度；

(2)、如图2，若∠ABC的角平分线BE交DC于点E，且BE//AD，试求出∠C的度数；

(3)、①如图3，若∠ABC和∠DCB的角平分线交于点E，试求出∠BEC的度数；
②在①的条件下，若延长BA、CD交于点F（如图4）．将原来条件“∠A＝140°，∠D＝80°”改为“∠F＝40°”．其他条件不变．则∠BEC的度数为．

查看试题解析
26. 乘法公式的探究及应用：
数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b、宽为a的长方形．并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．

(1)、请用两种不同的方法表示图2大正方形的面积．
方法1：；
方法2：；

(2)、观察图2，请你写出下列三个代数式： ${(a + b)}^{2}$ ， $a^{2} + b^{2}$ ， $a b$ 之间的数量关系：；

(3)、根据（2）题中的等量关系，解决如下问题：
①已知： $a + b = 5$ ， $a^{2} + b^{2} = 21$ ，求 $a b$ 的值；
②已知 ${(2022 - a)}^{2} + {(a - 2020)}^{2} = 10$ ，求 $(2022 - a) (a - 2020)$ 的值．

查看试题解析
27. 【知识回顾】
七年级学习代数式求值时，遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关，求a的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含x项的系数为0，即原式＝（a+3）x﹣6y+5，所以a+3＝0，则a＝﹣3．
【理解应用】

(1)、若关于x的多项式（2x﹣3）m+2m²﹣3x的值与x的取值无关，求m值；

(2)、已知A＝（2x+1）（x﹣1）﹣x（1﹣3y），B＝﹣x²+xy﹣1，且3A+6B的值与x无关，求y的值；

(3)、【能力提升】
7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为S₁ ，左下角的面积为S₂ ，当AB的长变化时，S₁﹣S₂的值始终保持不变，求a与b的等量关系．

查看试题解析