江苏省无锡市江阴市2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、（a³）²=a⁵ B、（a-b）²=a²-b² C、a・a³=a⁴ D、（-3a）³=-9a³

查看试题解析
2. 下列各式从左到右的变形，是因式分解的是（）

A、x²-9+6x=（x+3）（x-3）+6x B、x²-8x+16=（x-4）² C、（x+5）（x-2）=x²+3x-10 D、6ab=2a•3b

查看试题解析
3. 若a＝－0.3² ， b＝－3^－² ， c＝（－ $\frac{1}{3}$ )^－² ， d＝（－ $\frac{1}{3}$ )⁰ ，则它们的大小关系是（）

A、a<c<b<d B、b<a<d<c C、a<b<d<c D、b<a<c<d

查看试题解析
4. 一个三角形的两边长分别是1和3，则第三边的长可能是（）

A、1 B、2 C、3 D、7

查看试题解析
5. 一个多边形的外角和是360°，这个多边形是（）

A、四边形 B、五边形 C、六边形 D、不确定

查看试题解析
6. 如图，∠1＝∠2，∠DAB＝∠BCD.给出下列结论：①AB∥DC；②AD∥BC；③∠B＝∠D；④∠D＝2∠DAB.其中，正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 若 $M = (x - 2) (x - 5)$ ， $N = (x - 3) (x - 4)$ ，则 $M$ 与 $N$ 的大小关系为（）

A、 $M > N$ B、 $M = N$ C、 $M < N$ D、由 $x$ 的取值而定

查看试题解析
8. 若关于x、y的方程 ${\begin{matrix} 3x+y=1 + 3 a \\ x+3y= 1 -a \end{matrix}$ 的解满足x+y= 0，则a的值为（）

A、-I B、-2 C、0 D、不能确定

查看试题解析
9. 将 $Δ A B C$ 沿 $D E 、 E F$ 翻折，顶点 $A ， B$ 均落在点 $O$ 处，且 $E A$ 与 $E B$ 重合于线段 $E O$ ，若 $∠ C D O + ∠ C F O = 106^{0}$ ，则 $∠ C$ 的度数（）

A、40° B、37° C、36° D、32°

查看试题解析
10. 如图，已知D、E分别为△ABC的边AC、BC的中点，AF为△ABD的中线，连接EF，若四边形AFEC的面积为15，且AB＝8，则△ABC中AB边上高的长为（）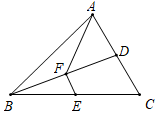

A、3 B、6 C、9 D、无法确定

查看试题解析

二、填空题

11. 最薄的金箔的厚度为 $0.000000091 m$ ，用科学记数法表示为 $m$ .

查看试题解析
12. 10^m= 3，10ⁿ= 5，则 $10^{3 m - n}$ =

查看试题解析
13. 已知二元一次方程2x-3y=5有一组解为 ${\begin{matrix} x = m \\ y = 1 \end{matrix}$ ，那么m=.

查看试题解析
14. 多项式 $4 a^{2} + 9$ 加上一个单项式后，可化为一个整式的平方，则这个单项式是.（写一个即可）

查看试题解析
15. 若已知x（x-1）-（x²-y）=-2.则 $\frac{x^{2} + y^{2}}{2} - x y$ =.

查看试题解析
16. 已知a ， b ， c是三角形的三边长，化简： $| a - b + c | - | a - b - c | =$ ．

查看试题解析
17. 在计算 $(x + y) (x - 3 y) - m y (n x - y)$ （m、n均为常数）的值，在把x、y的值代入计算时，粗心的小明把y的值看错了，其结果等于9，细心的小红把正确的x、y的值代入计算，结果恰好也是9，为了探个究竟，小红又把y的值随机地换成了2018，结果竟然还是9，根据以上情况，探究其中的奥妙，计算mn=.

查看试题解析
18. 把长都是宽的两倍的1个大长方形纸片和4个相同的小长方形纸片按图①、图②方式摆放，则图②中的大长方形纸片未被4个小长方形纸片覆盖部分的面积为cm².

查看试题解析

三、解答题

19. 计算：

(1)、 $3^{- 1} + {(π - 2019)}^{0} + | - \frac{2}{3} |$

(2)、 ${(- 2 x^{2})}^{3} + x^{2} \cdot x^{4} - {(- 3 x^{3})}^{2}$

(3)、 $(x + 2 y - 3) (x - 2 y + 3)$

查看试题解析
20. 把下面各式分解因式：

(1)、8a³b²-12ab³c

(2)、4m²-16n²

(3)、（x²+2x）²+2（x²+2x）+1

查看试题解析
21. 解方程组

(1)、 ${\begin{matrix} y = 2 x - 3 \\ 4 x - 3 y = 1 \end{matrix}$ （代入法）；

(2)、 ${\begin{matrix} 3 x - y = 5 \\ 5 x + 2 y = 23 \end{matrix}$ （加减法）

查看试题解析
22. 先化简，再求值： ${(x + y)}^{2} - 2 x (x + 3 y) + (x + 2 y) (x - 2 y)$ ，其中x=﹣1，y=2.

查看试题解析
23. 如图，在边长为1个单位的正方形网格中，△ABC经过平移后得到△A′B′C′，图中标出了点B的对应点B′．根据下列条件，利用网格点和无刻度的直尺画图并解答相关的问题（保留画图痕迹）：

（ 1 ）在给定方格纸中画出平移后的△A'B'C'；

（ 2 ）画出AB边上的中线CD；

（ 3 ）画出BC边上的高线AE；

（ 4 ）△A'B'C'的面积为____ ；
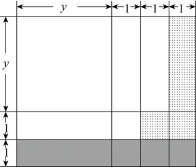
（ 5 ）在图中能使S△PAC＝S△ABC的格点P的个数有个（点P异于点B）．

查看试题解析
24. 如图，已知 $∠ A D B = ∠ B C E$ ， $∠ C A D + ∠ E = 180 °$ .

(1)、判断 $A C$ 与 $E F$ 的位置关系，并说明理由；

(2)、若 $C A$ 平分 $∠ B C E$ ， $E F ⊥ A F$ 于点 $F$ ， $∠ A D B = 80 °$ ，求 $∠ B A D$ 的度数.

查看试题解析
25. 提出问题：怎么运用矩形面积表示（y+2）（y+3）与2y+5的大小关系（其中y>0）？
几何建模：
（1）画长y+3，宽y+2的矩形，按图方式分割
（2）变形：2y+5=（y+2）+（y+3）
（3）分析：图中大矩形的面积可以表示为（y+2）（y+3）；阴影部分面积可以表示为（y+3）×1，画点部分的面积可表示为y+2，由图形的部分与整体的关系可知：

（y+2）（y+3）＞（y+2）+（y+3），即（y+2）（y+3）＞2y+5

归纳提炼：

当a>2，b>2时，表示ab与a+b的大小关系．根据题意，设a=2+m，b=2+n（m>0，n>0），要求参照上述研究方法，画出示意图，并写出几何建模步骤（用铅笔画图，并标注相关线段的长）

查看试题解析
26. 长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况.如图，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视.若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足3^a=27=3²·3^b.假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN=45°

(1)、求a、b的值；

(2)、若灯B射线先转动20秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？

(3)、如图2，两灯同时转动，在灯A射线到达AN之前.若射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，∠BCD：∠BAC.

查看试题解析