江苏省泰州市姜堰区2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、x²·x³=x⁶ B、a³+a³=2a⁶ C、（-2x³）²=-4x⁵ D、（-m）⁵÷（-m）³= m²

查看试题解析
2. 下列等式从左到右的变形中，属于因式分解的是（）

A、ab+ac+d=a（b+c）+d B、（x+1）（x+3）=x²+4x+3 C、6ab=2a·3b D、x（x-y）+y（y-x）=（x-y）²

查看试题解析
3. 若∠1与∠2是同旁内角，则（）

A、∠1与∠2不可能相等 B、∠1与∠2一定互补 C、∠1与∠2可能互余 D、∠1与∠2一定相等

查看试题解析
4. 代数式5⁵+5⁵+5⁵+5⁵+5⁵化简的结果是（）

A、5² B、5⁵ C、5⁶ D、5+5⁵

查看试题解析
5. 若代数式x²-4x+a可化为（x-b）²-1，则a+b是（）

A、5 B、4 C、3 D、2

查看试题解析
6. 如图，将木条a，b与c钉在一起，∠1=100°，∠2=60°．若木条a、b、c所在的直线围成直角三角形，则木条a顺时针旋转的度数不可能是（）

A、110° B、120° C、170° D、290°

查看试题解析

二、填空题

7. 预防新型冠状病毒感染要用肥皂勤洗手，已知肥皂泡的厚度约为0.0000007m，将数据0.0000007用科学记数法表示为．

查看试题解析
8. 计算：4²ⁿ·（ $- \frac{1}{4}$ ）²ⁿ⁺¹=（n为正整数）．

查看试题解析
9. 二元一次方程2x＋y＝5的正整数解为．

查看试题解析
10. 如图，铅笔放置在△ABC的边AB上，笔尖方向为点A到点B的方向，把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后，笔尖方向变为点B到点A的方向，这种变化说明．

查看试题解析
11. 如图，方格中的点A、B、C、D、E称为“格点”（格线的交点），以这5个格点中的3点为顶点画三角形，共可以画个直角三角形．

查看试题解析
12. 已知8x·16y=4，则3x+4y= ．

查看试题解析
13. 整式mx+n的值随x的取值不同而不同，下表是当x取不同值时对应的整式的值：则关于x的方程﹣mx+n=8的解为．
x
-2
-1
0
1
2
mx+n
7
5
3
1
-1

查看试题解析
14. 若方程组 ${\begin{array}{l} x - 2 m = 3 \\ 2 + y = m \end{array}$ ，则у= ．（用含x的代数式表示）

查看试题解析
15. 如图，△ABC的中线BD、CE相交于点F，若四边形AEFD的面积为6，则△CBF的面积为．

查看试题解析
16. 如图，正n边形A₁A₂A₃……An（每条边相等，每个内角都相等）竖立于地面，一边与地面重合，一束太阳光平行照射在正n边形上，若∠1-∠2=36°，则n= ．

查看试题解析

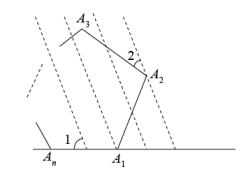
三、解答题

17. 计算：

(1)、（-3）⁰+（-1）²⁰⁰-3× $(- \frac{1}{3})^{- 2}$

(2)、（-2a²）³·a³-6a¹²÷（-3a³）

查看试题解析
18. 因式分解：

(1)、4x²-64

(2)、2x³y+4x²y²+2xy³

查看试题解析
19. 解方程组：

(1)、 ${\begin{array}{l} y = 2 x - 3 \\ 5 x - y = 3 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{2} + \frac{y}{3} = 16 \\ \frac{x}{3} - \frac{y}{4} = 5 \end{array}$

查看试题解析
20. 先化简，再求值：（a+b）（b-a）-a（a-2b）+（a-2b）² ，其中a=﹣1，b= $\frac{1}{5}$ ．

查看试题解析
21. 如图，在正方形网格中有一个格点三角形ABC（ABC的各顶点都在格点上，小正方形的边长为1）．

(1)、画出△ABC中边BC上的高线AD；（提醒：别忘了标注字母）

(2)、平移△ABC一次，使点A到点A₁ ，画出平移后的△A₁B₁C₁；

(3)、若连接AA₁、BB₁ ，则这两条线段的关系是．

(4)、△ABC平移一次到△A₁B₁C₁的过程中，线段AB扫过的区域面积是．

查看试题解析
22. 如图，这是一根断裂的木条，爱好数学的小明用量角器量得∠B=120°，∠C=110°，∠D=130°，于是小明得出木条的对边AB $∥$ ED，小明的判断对吗?为什么?

查看试题解析
23. 如果一个正整数能表示为两个连续奇数的平方差，那么称这个正整数为“友好数”．如：①8=3²-1²；②16=5²-3²；③24=7²-5² ，因此8，16，24 都是“友好数”．

(1)、48是“友好数”吗?为什么?

(2)、若一个“友好数”能表示为两个连续奇数2k+1和2k-1（k为正整数）的平方差，则这个“友好数”是8的倍数吗?为什么?

查看试题解析
24. 如图，在△ABC中，E、G分别是AB、AC上的点，F、D是BC上的点，连接EF、AD、DG，AD $∥$ EF，∠1+∠2=180°．

(1)、说明：AB $∥$ DG；

(2)、若∠2=145°，∠B=35°，说明：DG是∠ADC的平分线．

查看试题解析
25. 将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形，1号正方形的边长为x，2号正方形的边长为y．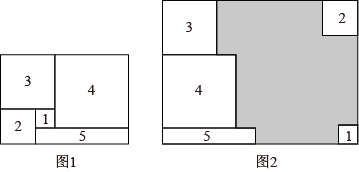

(1)、求5号长方形的面积（用含x，y的代数式表示）；

(2)、若图1中长方形的周长为24．
①若2号正方形与1号正方形的面积差为3，求5号长方形的面积；
②将图1中的1号、2号、3号、4号四个正方形和5号长方形按图2的方式放入周长为40的长方形中，则没有覆盖的阴影部分的周长为 ▲ ．

查看试题解析
26. 如图，△ABC中，∠ACB=90°，点D、E分别在边AC、AB上运动（不与顶点重合），点F在线段CD上（不与点D、C重合），射线ED与射线BF相交于点G．

(1)、如图1，若DE $∥$ BC，∠EDB=2∠G，说明：BG平分∠DBC．

(2)、如图2，若∠EDB=m∠ADB，∠DBG=n∠DBC，∠G=45°．
①若m= $\frac{5}{12}$ ， n= $\frac{1}{6}$ ，求∠DBC的值．
②若n= $\frac{1}{2}$ ，求m的值．
③若3m-n=1且m≠ $\frac{1}{2}$ ，求∠DBC的度数．

查看试题解析

x	-2	-1	0	1	2
mx+n	7	5	3	1	-1