江苏省南京市鼓楼区2021-2022学年七年级下学期期中数学试卷
试卷更新日期:2022-08-23 类型:期中考试
一、单选题
-
1. 下列图形中,可以由其中一个图形通过平移得到的是( )A、
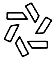 B、
B、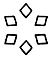 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、 ( )3. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、4. 已知一个n边形的每个外角都等于 ,则n的值是A、5 B、6 C、7 D、85. 如图, ,若 , , , 则下列说法正确的是( )
2. 下列运算正确的是( )A、 B、 C、 D、 ( )3. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、4. 已知一个n边形的每个外角都等于 ,则n的值是A、5 B、6 C、7 D、85. 如图, ,若 , , , 则下列说法正确的是( ) A、 B、 C、 D、6. 如图,四边形中, , 与、相邻的两外角平分线交于点E,若 , 则的度数为( )
A、 B、 C、 D、6. 如图,四边形中, , 与、相邻的两外角平分线交于点E,若 , 则的度数为( )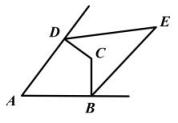 A、45° B、60° C、40° D、50°
A、45° B、60° C、40° D、50°二、填空题
-
7. 因式分解的结果是 .8. 计算:(﹣4)20×0.2518= .9. 如图,木工用角尺画出 , 其依据是 .
 10. 如图,在△ABC中,∠BAC=60°,∠1=∠2,则∠APB=°.
10. 如图,在△ABC中,∠BAC=60°,∠1=∠2,则∠APB=°. 11. 如图,已知 , 则 .
11. 如图,已知 , 则 . 12. 若 , 则代数式的值等于 .13. 如图,∠ABC=100°, , 动点P在射线BA上从点B开始沿BA方向运动,连接MP,当∠PMN=120°时,∠BPM的度数为 .
12. 若 , 则代数式的值等于 .13. 如图,∠ABC=100°, , 动点P在射线BA上从点B开始沿BA方向运动,连接MP,当∠PMN=120°时,∠BPM的度数为 .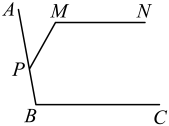 14. 代数式(个相加,为正整数)化简的结果是 .15. 如图是 A 型卡片(边长a的正方形)、B 型卡片(长为 a、宽为 b的长方形)、C 型卡片(边长为 b的正方形).现有 4张 A卡片,11张 B卡片,7张 C卡片,选用它们无缝隙、无重叠地拼正方形或长方形,下列说法正确的是 . (只填序号)
14. 代数式(个相加,为正整数)化简的结果是 .15. 如图是 A 型卡片(边长a的正方形)、B 型卡片(长为 a、宽为 b的长方形)、C 型卡片(边长为 b的正方形).现有 4张 A卡片,11张 B卡片,7张 C卡片,选用它们无缝隙、无重叠地拼正方形或长方形,下列说法正确的是 . (只填序号)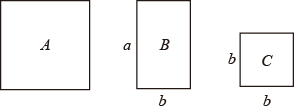
①可拼成边长为的正方形;
②可拼成边长为的正方形;
③可拼成长、宽分别为、的长方形;
④用所有卡片可拼成一个大长方形.
16. 如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是.
三、解答题
-
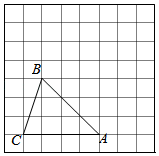
17. 计算:(1)、(2)、18. 把下列各式分解因式;(1)、;(2)、 .19. 先化简,再求值: , 其中 .20. 如图,方格纸中每一个小方格的边长为1个单位,△ABC的顶点都在方格纸的格点上.
 (1)、画出将△ABC向右平移2个单位,再向上平移3个单位得到的△A1B1C1(点A1、B1、C1分别是点A、B、C的对应点);(2)、连接AA1、BB1 , 则线段AA1、BB1的位置关系为;(3)、试在边AC上确定点P,连接BP,使BP平分△ABC的面积(要求:在图中画出线段BP).21. 如图,四边形中, , 作于点 , 设分别与、交于点、 . 若平分 , 且 , 求证: .
(1)、画出将△ABC向右平移2个单位,再向上平移3个单位得到的△A1B1C1(点A1、B1、C1分别是点A、B、C的对应点);(2)、连接AA1、BB1 , 则线段AA1、BB1的位置关系为;(3)、试在边AC上确定点P,连接BP,使BP平分△ABC的面积(要求:在图中画出线段BP).21. 如图,四边形中, , 作于点 , 设分别与、交于点、 . 若平分 , 且 , 求证: .
完成下面的证明过程:
证明:∵ , ∴ ,
∵平分 , ∴ ,
,
∴ (等量代换),
∴( ),
∴ (两直线平行,内错角相等),
∴( ),
∵ , ∴
∴( ),
又∵ ,
∴(等量代换).
22. 有些同学会想当然地认为 .(1)、举出反例说明该式不一定成立;(2)、计算;(3)、直接写出当、满足什么条件,该式成立.23. 如图,在△ABC中,AD是角平分线,E为边AB上一点,连接DE,∠EAD=∠EDA,过点E作EF⊥BC垂足为F. (1)、DE与AC平行吗?请说明理由;(2)、若∠BAC=95°,∠B=35°,求∠DEF的度数.24. 如图1,是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块相同的小长方形,然后拼成一个正方形(如图2).
(1)、DE与AC平行吗?请说明理由;(2)、若∠BAC=95°,∠B=35°,求∠DEF的度数.24. 如图1,是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块相同的小长方形,然后拼成一个正方形(如图2). (1)、用两种不同的方法表示图2中阴影部分的面积:
(1)、用两种不同的方法表示图2中阴影部分的面积:方法1:S阴影= .
方法2:S阴影= .
(2)、写出(a+b)2 , (a﹣b)2 , ab这三个代数式之间的等量关系为 .(3)、①若(2m+n)2=14,(2m﹣n)2=6,则mn的值为 ▲ .②已知x+y=10,xy=16,求x﹣y的值.
25. 如图,已知直线AB∥CD,直线EF分别与AB,CD交于O点,G点.P点是直线EF上的一个动点. (1)、如图1,当运动至与之间时,过点作分别交 , 于 , . 若 , 则度.(2)、如图2,当运动至直线上方时,过点作分别交 , 于、N.作的角平分线并反向延长交于点 , 交于点 , 作的角平分线与交于点 , 若 , 求的度数.(3)、过点作分别交 , 于 , , 设与交于点 , 点在、之间且MO: , . 沿直线方向平移直线 , 并保持始终在下方,使得 . 连接、、 . 在备用图中画出相关图形,并直接写出的面积.26. 阅读下面材料:小亮遇到这样问题:如图1,已知 , EOF是直线AB、CD间的一条折线.判断、、三个角之间的数量关系.小亮通过思考发现:过点O作 , 通过构造内错角,可使问题得到解决.
(1)、如图1,当运动至与之间时,过点作分别交 , 于 , . 若 , 则度.(2)、如图2,当运动至直线上方时,过点作分别交 , 于、N.作的角平分线并反向延长交于点 , 交于点 , 作的角平分线与交于点 , 若 , 求的度数.(3)、过点作分别交 , 于 , , 设与交于点 , 点在、之间且MO: , . 沿直线方向平移直线 , 并保持始终在下方,使得 . 连接、、 . 在备用图中画出相关图形,并直接写出的面积.26. 阅读下面材料:小亮遇到这样问题:如图1,已知 , EOF是直线AB、CD间的一条折线.判断、、三个角之间的数量关系.小亮通过思考发现:过点O作 , 通过构造内错角,可使问题得到解决. (1)、请回答:、、三个角之间的数量关系是 .(2)、如图2,将沿BA方向平移到(B、、E共线), , AC与DF相交于点G,GP、EP分别平分、相交于点P,求的度数;(3)、如图3,直线 , 点B、F在直线m上,点E、在直线n上,连接并延长至点A,连接BA、BC和CA,做和的平分线交于点M,若 , 则(直接用含的式子表示).
(1)、请回答:、、三个角之间的数量关系是 .(2)、如图2,将沿BA方向平移到(B、、E共线), , AC与DF相交于点G,GP、EP分别平分、相交于点P,求的度数;(3)、如图3,直线 , 点B、F在直线m上,点E、在直线n上,连接并延长至点A,连接BA、BC和CA,做和的平分线交于点M,若 , 则(直接用含的式子表示).