湖北省武汉市青山区2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标，其中，可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点A（2，﹣3）位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 4的算术平方根是（）

A、-2 B、2 C、 $\pm 2$ D、 $\sqrt{2}$

查看试题解析
4. 在3.14， $\frac{22}{7}$ ，－ $\sqrt{5}$ ， $\sqrt[3]{64}$ ， $\frac{π}{2}$ ， 1.01001000100001这六个数中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，直线a，b被直线c所截，下列条件中，不能判定a∥b（）

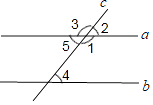A、∠2=∠4 B、∠1+∠4=180° C、∠5=∠4 D、∠1=∠3

查看试题解析
6. 下列各式错误的是（）

A、 $\sqrt{2^{2}}$ ＝2 B、 $\sqrt[3]{- 0.001}$ ＝－0.1 C、 $\sqrt{(- 2)^{2}}$ ＝±2 D、 $\sqrt[3]{- 5}$ ＝－ $\sqrt[3]{5}$

查看试题解析
7. 已知A点的坐标为（3，a＋3），B点的坐标为（a，4），AB∥x轴，则线段AB的长为（）

A、5 B、4 C、3 D、2

查看试题解析
8. 如图，将一张长方形纸片按如图所示的方式沿虚线折叠，得到两个面积分别为16和5的正方形，则阴影部分的面积为（）

A、4 $\sqrt{5}$ －5 B、3 $\sqrt{5}$ C、4－ $\sqrt{5}$ D、4＋ $\sqrt{5}$

查看试题解析
9. 下列命题中，真命题的个数有（）
①同旁内角互补：②两个无理数的和一定是无理数：③±4是64的立方根：④过一点有且只有一条直线与已知直线平行．

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 如图，长为50m，宽为30m的长方形地块上，有纵横交错的几条小路，宽均为1m，其它部分均种植草坪，则种植草坪的面积为（）

A、1344m² B、1421m² C、1431m² D、1341m²

查看试题解析

二、填空题

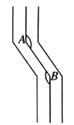
11. 实数－ $\sqrt{5}$ 的相反数是．

查看试题解析
12. 已知点P（x＋2，2x－3）在y轴上，则x＝．

查看试题解析
13. 若一个数的平方根就是它本身，则这个数是．

查看试题解析
14. 如图，一条公路两次转弯后，和原来的方向相同．如果第一次的拐角∠A的度数为130°，第二次拐角∠B的度数为．

查看试题解析
15. 如图，在平面直角坐标系中，点A在x轴上，点B（0，9），线段AB向右平移3个单位至线段CD，线段CD与y轴交于点E，若图中阴影部分面积是21，则点C的坐标为．

查看试题解析
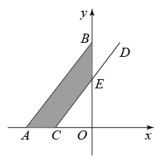16. 如图，已知AB∥CD，E、F、H分别为AB、CD、AC上一点（∠DFK＜∠BEK），KG平分∠EKF，∠AEK＋∠HKE＝180°．则下列结论：①CD∥KH；②∠BEK＋∠DFK＝2∠EKG；③∠BEK－∠DFK＝∠GKH；④∠BAC＋∠AGK－∠GKF＋∠DFK＝180°．其中正确的是．（填序号）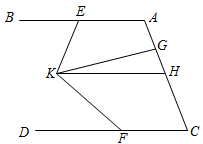

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{\frac{49}{25}}$ － $\sqrt[3]{- 1}$ ；

(2)、| $\sqrt{2}$ － $\sqrt{3}$ |＋2 $\sqrt{2}$ ．

查看试题解析
18. 解方程：

(1)、 $(x － 1)^{2} ＝ 9$ ；

(2)、 $8 x^{3} － 27 ＝ 0$ ．

查看试题解析
19. 请根据条件进行推理，得出结论，并在括号内注明理由．
已知：如图，∠1＝∠2，∠B＋∠CDE＝180°．

求证：AB∥CD．

证明：∵∠1＝   （    ）

又∵∠1＝∠2

∴∠BFD＝∠2（   ）

∴BC∥   （    ）

∴∠C＋＝180°（    ）

又∵∠B＋∠CDB＝180°

∴∠B＝∠C

∴AB∥CD（    ）．

查看试题解析
20. 如图，直线EF、CD相交于点O，OA⊥OB，OC平分∠AOF．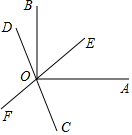

(1)、直接写出∠DOF的对顶角和邻补角；

(2)、若∠AOE＝30°，求∠BOD的度数．

查看试题解析
21. 如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均在格点上．

(1)、请建立合适的平面直角坐标系，使点A，点B的坐标分别为A（－1，3）、B（3，1），并写出点C的坐标；

(2)、在（1）的条件下．
①若△ABC中任意一点P（a，b）平移后对应点为P（a＋2，b－5），将△ABC作同样的平移得到△A₁B₁C₁ ．请画出平移后的△A₁B₁C₁；
②点Q为y轴上一动点，当AQ＋BQ最小时，直接写出点Q的坐标．

查看试题解析
22. 某小区有一个由实木栅栏围成的400m²的正方形室外阅读场地，现在要将其改建成300m²的长方形场地，且长和宽之比为3：2．

(1)、求这个长方形场地的长宽分别是多少m？

(2)、如果要把原来围成正方形场地的实木栅栏利用起来，围成这个长方形场地，那么这些实木栅栏是否够用？并说明理由．

查看试题解析
23. 已知，直线AB∥CD，点E、F分别在直线AB、CD上，点P是直线AB与CD外一点，连接PE、PF．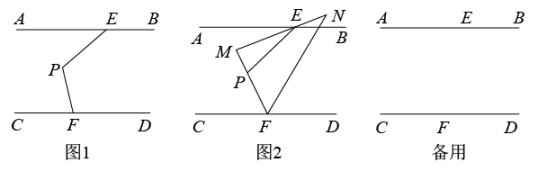

(1)、如图1，若∠AEP＝45°，∠DFP＝105°，求∠EPF的度数：

(2)、如图2，过点E作∠AEP的角平分线EM交FP的延长线于点M，∠DFP的角平分线FN交EM的反向延长线于点N，若∠M与3∠N互补，试探索直线EP与直线FN的位置关系，并说明理由；

(3)、若点P在直线AB的上方且不在直线EF上，作∠DFP的角平分线FN交∠AEP的角平分线EM所在直线于点N，请直接写出∠EPF与∠ENF的数量关系．

查看试题解析
24. 已知，点A在y轴正半轴上，OA＝a，点B位于第二象限，且点B到两坐标轴的距离均为b，其中a、b满足b＝ $\sqrt{a - 2}$ ＋ $\sqrt{4 - 2 a}$ ＋4．

(1)、a＝， b＝；

(2)、点C在x轴的负半轴上，射线CD∥AB．
①如图1，过C作射线CE交y轴于点E，使∠DCE＝3∠ECO，过A作射线AF交CE于点F，使∠BAF＝3∠OAF，求∠AFE的度数；
②如图2，设点C的坐标为（m，0），射线CD上点P的坐标为（n，1），试探索m与n的数量关系，并说明理由．

查看试题解析