（北师大版）2022-2023学年度第一学期七年级数学第4章 基本平面图形 单元测试
试卷更新日期：2022-08-23 类型：单元试卷
一、单选题
-
1. 经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，这一实际问题应用的数学知识是（ ）A、两点确定一条直线 B、两点之间直线最短 C、两点之间线段最短 D、直线有两个端点2. 下列说法正确的是（ ）A、射线 与射线 是同一条射线 B、射线 的长度是 C、直线 ， 相交于点 D、两点确定一条直线3. 如图，D是线段AB上的一点，点C是AB的中点， ， ， 则（ ）
A、1 B、2 C、3 D、64. 如图，将三角形纸板 沿虚线 剪去一部分，我们发现剩下的四边形的周长小于原三角形的周长，正确解释这一现象的数学知识是（ ）
A、两点确定一条直线 B、两点之间，线段最短 C、垂线段最短 D、经过直线外一点，有且只有一条直线与已知直线平行5. 如图，∠ACB可以表示为（ ）
A、∠1 B、∠2 C、∠3 D、∠46. 下午14时整，钟表的时针与分针构成的角度是（ ）A、30° B、60° C、90° D、120°7. 下列各角中，为锐角的是（ ）A、 平角 B、 周角 C、 直角 D、 周角8. 如图，甲从A处出发沿北偏东60°方向走向B处，乙从A处出发沿南偏西30°方向走到C处，则∠BAC的度数是 （ ）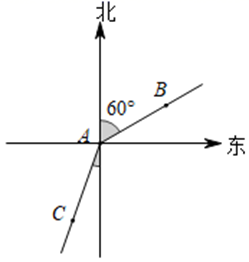
A、 B、 C、 D、9. 从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成10个三角形，则n的值是（ ）A、10 B、11 C、12 D、1310. 过多边形一个顶点的所有对角线把这个多边形分成了7个三角形，则这个多边形的边数是（ ）A、8 B、9 C、10 D、11二、填空题
-
11. 在日常生活和生产中有很多现象可以用数学知识进行解释．如图，要把一根挂衣帽的挂钩架水平固定在墙上，至少需要钉个钉子．用你所学数学知识说明其中的道理 ．
12. 已知点C在线段AB上，点D、E分别是AC和BC的中点，若 ， 则cm．13. 下午两点半时，时钟的时针和分针的夹角是°.14. 如图，已知OD平分∠AOC，OE平分∠COB，∠AOD＝20°，∠EOB＝40°.则∠AOB＝.
15. 从一个多边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形被分割成2018个三角形，则这个多边形的边数为.三、解答题
-
16. 计算：
（1）22°18′×5；
（2）90°﹣57°23′27″．
17. 如图，已知线段AB，请用尺规按照下列要求作图：①延长线段AB到C，使得BC=2AB；
②连接PC；
③作射线AP．
如果AB=2cm，求AC的值
18. 已知线段AB=10cm，在直线AB上有一点C，且BC=4cm，点D是线段AC的中点，试求线段AD的长.19. 如图，点C为线段AB的中点，点D在线段CB上，若AD＝3cm，DB＝2cm，求CD的长．
请将下面的解题过程补充完整：
解：因为AD＝3cm，DB＝2cm．
所以 ▲ ＝AD＋DB＝3＋2＝5（cm）．
因为点C为线段AB的中点，所以 ▲ ＝ ▲ cm．
所以CD＝ ▲ － ▲ ＝ ▲ cm．
20. 读句画图填空：（1）画∠AOB；
（2）作射线OC，使∠AOC=∠AOB；
（3）由图可知，∠BOC= ∠AOB．
21. 补全解题过程．已知：如图，∠AOB＝40°，∠BOC＝70°，OD平分∠AOC．
求∠BOD的度数．
解：∵∠AOB＝40°，∠BOC＝70°，
∴∠AOC＝∠AOB＋∠BOC＝ ▲ °．
∵OD平分∠AOC，
∴∠AOD＝∠ ▲ （ ▲ ）（填写推理依据）．
∴∠AOD＝ ▲ °．
∴∠BOD＝∠AOD﹣∠ ▲ ．
∴∠BOD＝ ▲ °．
