（北师大版）2022-2023学年度第一学期七年级数学3.5探索与表达规律同步测试

试卷更新日期：2022-08-22 类型：同步测试

进入出卷网下载

一、单选题

1. 如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2021个格子中的数为（）

-1

a

b

c

2

5

…

A、-1 B、0 C、2 D、5

查看试题解析
2. 如图是一组有规律的图案，它们是由边长相同的黑白两种颜色的小正方形组成的，按照这样的规律，若组成的图案中有2021个黑色小正方形，则这个图案是（）

A、第505个 B、第506个 C、第507个 D、第508个

查看试题解析
3. 观察下列两列数：
第一列：2，4，6，8，10，12，……

第二列：2，5，8，11，14，17，……

通过探究可以发现，第1个相同的数是2，第2相同的数是8，…….则第2022个相同的数在第一列中是第（）个

A、6062 B、6064 C、6066 D、6068

查看试题解析
4. 下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有4个小圆圈，第②个图形中一共有10个小圆圈，第③个图形中一共有19个小圆圈，…，按此规律排列，则第⑥个图形中小圆圈的个数为（）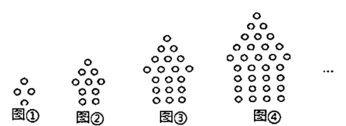

A、31 B、46 C、64 D、85

查看试题解析
5. 已知整数 $a_{1}$ 、 $a_{2}$ 、 $a_{3}$ 、 $a_{4}$ 、……满足下列条件： $a_{1} = - 1$ ， $a_{2} = - | a_{1} + 2 |$ ， $a_{3} = - | a_{2} + 3 |$ ， $a_{4} = - | a_{3} + 4 |$ ， …， ${a_{n}}_{+ 1} = - | a_{n} + n + 1 |$ （n为正整数）依此类推，则 $a_{2022}$ 的值为（）

A、-1010 B、-2020 C、-1011 D、-2022

查看试题解析
6. 将一列有理数－1，2，－3，4，－5，6……按如图所示进行排列，则2022应排在（）

A、 $A$ 位置 B、 $B$ 位置 C、 $D$ 位置 D、 $E$ 位置

查看试题解析
7. 将全体自然数按下面的方式进行排列，按照这样的排列规律，2022应位于（）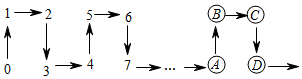

A、Ⓐ位 B、Ⓑ位 C、Ⓒ位 D、Ⓓ位

查看试题解析
8. 如图所示，直线 $A B ， C D$ 相交于点 $O$ ， “阿基米德曲线”从点 $O$ 开始生成，如果将该曲线与每条射线的交点依次标记为 $1 ， - 2 ， 3 ， - 4 ， 5 ， - 6$ …．那么标记为“ $2021$ ”的点在（）

A、射线 $O A$ 上 B、射线 $O B$ 上 C、射线 $O C$ 上 D、射线 $O D$ 上

查看试题解析
9. 一电子跳蚤在数轴上从原点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第2022次落下时，落点处表示的数为（）

A、－2022 B、2022 C、－1011 D、1011

查看试题解析
10. 计算：3¹+1 = 4，3² + 1 = 10，3³ + 1 = 28，3⁴ + 1 = 82，3⁵+1 = 244，…，归纳计算结果中的个位数字的规律，猜测3²⁰²¹ + 1的个位数字是（　　）

A、0 B、2 C、4 D、8

查看试题解析

二、填空题

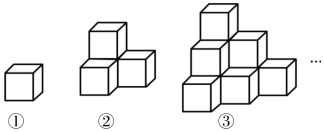
11. 如图所示的几何体都是由棱长为1个单位的正方体摆成的，经计算可得第①个几何体的表面积为6个平方单位，第②个几何体的表面积为18个平方单位，第③个几何体的表面积是36个平方单位，…依此规律，则第⑩个几何体的表面积是个平方单位.

查看试题解析
12. 如图，1条直线最多将平面分成2个部分，2条直线最多将平面分成4个部分，3条直线最多将平面分成7个部分，4条直线最多将平面分成11个部分，5条直线最多将平面分成16个部分，6条直线最多将平面分成22个部分，则49条直线最多将平面分成个部分.

查看试题解析

13. 观察下列表格中的每组数，根据规律得出

a + b

的值为.

第一组数	6	8	10
第二组数	8	15	17
第三组数	10	24	26
第四组数	12	35	37
…	…	…	…
…	24	a	b

查看试题解析

14. 小明同学利用计算机设计了一个程序，输入和输出的情况如下表。他发现从第三个输出项起的每一项都与这一项的前面两个输出项有关。按此规律，从1开始一直输入到 2022后，输出项的系数与次数均为奇数的项共有个.

输入	1	2	3	4	5	6	7	8	$\dots \dots$
输出	$a$	$3 b^{2}$	$4 a b^{2}$	$7 a b^{4}$	$11 a^{2} b^{6}$	$18 a^{3} b^{10}$	$29 a^{5} b^{16}$	$47 a^{8} b^{26}$	$\dots \dots$

查看试题解析

15. 如图，这是由相同大小的正方形和相同大小的圆按照一定规律摆放而成的，按此规律，则第（n）个图形中圆的个数为.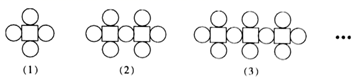

查看试题解析

三、解答题

16. 下面是按一定规律得到的一列数：
$\frac{1}{2} - (1 + \frac{1}{2}) = - 1$ ，第1个数是-1；

$\frac{1}{3} - (1 - \frac{1}{3}) = - \frac{1}{3}$ ，第2个数是 $- \frac{1}{3}$ ；

$\frac{1}{4} - (1 + \frac{1}{4}) = - 1$ ，第3个数是-1；

$\frac{1}{5} - (1 - \frac{1}{5}) = - \frac{3}{5}$ ，第4个数是 $- \frac{3}{5}$ ；

……

按照以上规律用算式分别表示出第8和第10个数，并比较这两个数的大小．

查看试题解析
17. 如图所示，由一些点组成形如三角形的图形，每条“边”（包括两个顶点）有 $n (n > 1)$ 个点，每个图形的总点数记为S ．

(1)、当 $n = 4$ 时，S的值为；当 $n = 6$ 时，S的值为；

(2)、每条“边”有n个点时的总点数S是（用含n的式子表示）；

(3)、当 $n = 2021$ 时，总点数S是多少？

查看试题解析
18. 用棋子摆出下列一组图形：

(1)、填写下表：

图形编号

1

2

3

4

5

6

图形中的棋子

6

(2)、照这样的方式摆下去，写出摆第 n 个图形棋子的枚数；

(3)、如果某一图形共有99枚棋子，你知道它是第几个图形吗？

查看试题解析
19. 有依次排列的3个数：3，9，8，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：3，6，9，﹣1，8，这称为第一次操作；做第二次同样的操作后也可产生一个新数串：3，3，6，3，9，﹣10，﹣1，9，8，继续依次操作下去．问：从数串3，9，8开始操作第一百次以后所产生的那个新数串的所有数之和是多少？

查看试题解析
20. 如果一个数等于它的不包括自身的所有因数之和，那么这个数就叫完全数.例如，6的不包括自身的所有因数为1，2，3，6=1+2+3，所以6是完全数.大约2200多年前，欧几里得提出：如果2ⁿ-1是质数，那么2^n-1·（2ⁿ-1）是一个完全数，请你根据这个结论写出6之后的下一个完全数.

查看试题解析
21. 请你首先阅读下面的材料，然后回答问题．
如果给你一段密码：L dp d vwxghqw，你知道它的意思吗？为了保密，许多情况下都要采用密码，这时就需要有破译密码的“钥匙”．对于上述密码，我们知道英语字母表中的字母是按以下顺序排列的：a b c d e f g h i j k l m n o p q r s t u v w x y z

如果规定a又接在z的后面，使26个字母排成圈．此时给你破译密码L dp d vwxghqw的钥匙为：x﹣3．你能够解读这段密码的意思了吗？请写出你的解读结果，并说明理由？

查看试题解析
22. 为了求 $1 + 3 + 3^{2} + 3^{3} + \cdot \cdot \cdot + 3^{100}$ 的值，可令M= $1 + 3 + 3^{2} + 3^{3} + \cdot \cdot \cdot + 3^{100}$ ，则 $3 M= 3 + 3^{2} + 3^{3} + \cdot \cdot \cdot + 3^{101}$ ，因此 $3 M-M= 2 M= 3^{101} - 1$ ，所以 $M= \frac{3^{101} - 1}{2}$ ，即 $1 + 3 + 3^{2} + 3^{3} + \cdot \cdot \cdot + 3^{100} = \frac{3^{101} - 1}{2}$ ，仿照以上推理计算： $1 {+5+5}^{2} {+5}^{3} + \cdot \cdot \cdot {+5}^{2019}$

查看试题解析
23. 一动点 $P$ 从数轴上的原点出发，沿数轴的正方向以每前进 $5$ 个单位、后退 $3$ 个单位的程序运动，已知点 $P$ 每秒前进或后退 $1$ 个单位，设 $x_{n}$ 表示第 $n$ 秒点 $P$ 在数轴上的位置所对应的数（如 $x_{4} = 4$ ， $x_{5} = 5$ ， $x_{6} = 4$ ），求 $x_{2011}$ 所对应的数.

查看试题解析
24. 探索规律：将连续的偶数2，4，6，8，…，排成如下表：

(1)、图中十字框中的五个偶数的和与中间的偶数16有什么关系？

(2)、移动十字架，设中间的偶数为x，用代数式表示十字框中的五个偶数的和；

(3)、若将十字框上下左右移动，可框住另外的五个偶数，则能框住五个偶数的和等于2010吗？如能写出这五个偶数；如不能，说明理由。

查看试题解析

图形编号	1	2	3	4	5	6
图形中的棋子	6

（北师大版）2022-2023学年度第一学期七年级数学3.5探索与表达规律 同步测试

一、单选题

二、填空题

三、解答题

（北师大版）2022-2023学年度第一学期七年级数学3.5探索与表达规律同步测试