福建省泉州市五校联考2021-2022学年高一上学期数学期中考试试卷

试卷更新日期：2022-08-22 类型：期中考试

进入出卷网下载

一、单选题

1. 若集合 $A = {x | x > 1}$ ， $B = {x | x^{2} - 2 x - 3 \leq 0}$ ，则 $A \cap B =$ （）

A、 $(1, 3]$ B、 $[1, 3]$ C、 $[- 1, 1)$ D、 $[- 1, + \infty)$

查看试题解析
2. 下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的为（）

A、y＝x^－⁴ B、y＝x^－¹ C、y＝x² D、y＝ $x^{\frac{1}{3}}$

查看试题解析
3. 函数 $f (x) = | x | - \frac{1}{x^{2}}$ 的图象大致形状是（）

A、 B、 C、 D、

查看试题解析
4. 已知函数f（x）定义域为（0，+∞），则函数F（x）＝f（x+2）+ $\sqrt{3 - x}$ 的定义域为（）

A、（﹣2，3] B、[﹣2，3] C、（0，3] D、（2，3]

查看试题解析
5. 已知命题：“ $\exists x \in R, x^{2} + a x - 4 a = 0$ ”为假命题，则实数a的取值范围为（）

A、 ${a | - 16 \leq a \leq 0}$ B、 ${a | - 16 < a < 0}$ C、 ${a | - 4 \leq a \leq 0}$ D、 ${a | - 4 < a < 0}$

查看试题解析
6. 《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架，其中卷第九勾股中记载：“今有邑，东西七里，南北九里，各中开门．出东门一十五里有木．问出南门几何步而见木?”其算法为：东门南到城角的步数，乘南门东到城角的步数，乘积作被除数，以树距离东门的步数作除数，被除数除以除数得结果，即出南门 $x$ 里见到树，则 $x = \frac{(9 \times \frac{1}{2}) \times (7 \times \frac{1}{2})}{15}$ ．若一小城，如图所示，出东门1200步有树，出南门750步能见到此树，则该小城的周长的最小值为（注：1里=300步）（）

A、 $2 \sqrt{10}$ 里 B、 $4 \sqrt{10}$ 里 C、 $6 \sqrt{10}$ 里 D、 $8 \sqrt{10}$ 里

查看试题解析
7. 已知 $f (x)$ 是定义在 $(2 a - 6 ， a)$ 上的奇函数，且 $f (x)$ 在 $[0 ， a)$ 上单调递减，则不等式 $f (3 x - 1) \leq f (1 - 4 x)$ 的解集为（）

A、 $(- \frac{1}{3} ， \frac{2}{7}]$ B、 $[\frac{2}{7} ， \frac{3}{4})$ C、 $[\frac{2}{7} ， 1)$ D、 $(- \frac{1}{4} ， \frac{2}{7}]$

查看试题解析
8. 正数 $a$ ， $b$ 满足 $9 a + b = a b$ ，若不等式 $a + b \geq - x^{2} + 2 x + 18 - m$ 对任意实数 $x$ 恒成立，则实数 $m$ 的取值范围是（）

A、 $m \geq 3$ B、 $m < 3$ C、 $m < 6$ D、 $m \geq 6$

查看试题解析
9. 已知 $f (x)$ 是定义域为R的函数，满足 $f (x + 1) = f (x - 3)$ ， $f (1 + x) = f (3 - x)$ ，当 $0 \leq x \leq 2$ 时， $f (x) = x^{2} - x$ ，则下列说法正确的是（）
① $f (x)$ 的最小正周期为4② $f (x)$ 的图像关于直线 $x = 2$ 对称③当 $0 \leq x \leq 4$ 时，函数 $f (x)$ 的最大值为2④ 当 $6 \leq x \leq 8$ 时，函数 $f (x)$ 的最小值为 $- \frac{1}{2}$

A、①②③ B、①② C、①②④ D、①②③④

查看试题解析

二、多选题

10. 已知集合A={4，a}，B={1，a²}，a∈R，则A∪B可能是（）

A、{-1，1，4} B、{1，0，4} C、{1，2，4} D、{-2，1，4}

查看试题解析
11. 设a，b∈R且ab >0，则下列不等式正确的是（）

A、 $a^{2} + b^{2} \geq 2 a b$ B、 $a + b \geq 2 \sqrt{a b}$ C、 $\frac{1}{a} + \frac{1}{b} \geq \frac{2}{\sqrt{a b}}$ D、 $\frac{b}{a} + \frac{a}{b} \geq 2$

查看试题解析
12. 有以下判断，其中是正确判断的有（）

A、 $f (x) = \frac{| x |}{x}$ 与 $g (x) = {\begin{array}{l} 1 ， x \geq 0 \\ - 1 ， x < 0 \end{array}$ 表示同一函数； B、函数 $y = f (x)$ 的图象与直线 $x = 1$ 的交点最多有 1 个 C、函数 $f (x) = x^{2} + 2 + \frac{1}{x^{2} + 2}$ 的最小值为 2 D、若 $f (x) = | x - 1 | - | x |$ ，则 $f (f (\frac{1}{2})) = 1$

查看试题解析

三、填空题

13. 已知函数 $f (x) = {\begin{array}{l} - x + 4, x \leq 0 \\ x^{2}, x > 0 \end{array}$ ，若 $f (m) = 4$ ，则 $m =$ ．

查看试题解析
14. 不等式 $\frac{x - 2}{x + 1} > 2$ 的解集是.

查看试题解析
15. 若p：x(x－3)<0是q：2x－3<m的充分不必要条件，则实数m的取值范围是．

查看试题解析
16. 已知偶函数 $f (x)$ 和奇函数 $g (x)$ 均定义在 $R$ 上，且满足 $f (x) + g (x) = 3 x^{2} - \frac{4 x}{x^{2} + 9} + 5$ ，则 $f (- 1) + g (3) =$ ．

查看试题解析

四、解答题

17. 已知集合 $A = {x | 2 ⩽ x ⩽ 6}$ ， $B = {x | 1 < x < 5}$ ， $C = {x | m < x < m + 1}$ ， $U = R$ ．

(1)、求 $A ∪ B$ ， $(∁_{U} A) ∩ B$ ；

(2)、若 $C \subseteq B$ ，求m的取值范围．

查看试题解析
18.

(1)、当 $x \in (0 ， \frac{1}{2})$ 时，求 $y = x (1 - 2 x)$ 的最大值；

(2)、设 $x \geq 2$ ，求函数 $y = \frac{x (x + 1)}{x - 1}$ 的最小值.

查看试题解析
19. 已知函数 $f (x)$ 是定义在R上的偶函数，当 $x$ ≥0时，有 $f (x) = \frac{4 x}{x + 4}$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、判断函数 $f (x)$ 在 $[0 ， + ∞)$ 上的单调性，并用定义证明.

查看试题解析
20. 某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的年收益 $f (x)$ 与投资额 $x$ 成正比，其关系如图1；投资股票等风险型产品的年收益 $g (x)$ 与投资额 $x$ 的算术平方根成正比，其关系如图2.

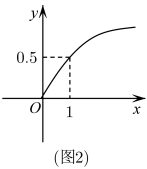(1)、分别写出两种产品的年收益 $f (x)$ 和 $g (x)$ 的函数关系式；

(2)、该家庭现有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大年收益，其最大年收益是多少万元？

查看试题解析
21. 在① $\forall x \in [- 2 ， 2]$ ， ② $\exists x \in [1 ， 3]$ 这两个条件中任选一个，补充到下面问题的横线中，并求解该问题.
已知函数 $f (x) = x^{2} + a x + 4$ .

(1)、当 $a = - 2$ 时，求 $f (x)$ 在 $[- 2 ， 2]$ 上的值域；

(2)、若_________， $f (x) \geq 0$ ，求实数 $a$ 的取值范围.
注：如果选择多个条件分别解答，则按第一个解答计分.

查看试题解析
22. 已知二次函数 $f (x) = a x^{2} + b x + c$ .

(1)、若 $f (x) > 0$ 的解集为 ${x | - 3 < x < 4}$ ，解关于 $x$ 的不等式 $b x^{2} + 2 a x - (c + 3 b) < 0$ .

(2)、若对任意 $x \in R$ ， $f (x) \geq 0$ 恒成立，求 $\frac{b}{a + c}$ 的最大值.

(3)、已知 $b = 4$ ， $a > c$ ，若 $f (x) \geq 0$ 对于一切实数 $x$ 恒成立，并且存在 $x_{0} \in R$ ，使得 $a x_{0}^{2} + b x_{0} + c = 0$ 成立，求 $\frac{4 a^{2} + c^{2}}{2 a - c}$ 的最小值.

查看试题解析