福建省龙岩市六县一中联考2021-2022学年高一上学期数学期中考试试卷
试卷更新日期:2022-08-22 类型:期中考试
一、单选题
-
1. 已知集合M={(x,y)|x,y∈N* , x+y<3},则M中元素的个数为( )A、1 B、2 C、3 D、02. 命题“ ”的否定为( )A、 B、 C、 D、3. 为安全燃放某种烟花,现收集到以下信息:
①此烟花导火索燃烧的速度是每秒0.6厘米;
②人跑开的速度为每秒4米;
③距离此烟花燃放点50米以外(含50米)为安全区.
为了使导火索燃尽时人能够跑到安全区,导火索的长度 (厘米)应满足的不等式为( )
A、 B、 C、 D、4. 已知 且 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件5. 已知a=0.60.6 , b=0.61.6 , c=1.60.6 , 则( )A、a>b>c B、a>c>b C、c>b>a D、c>a>b6. 函数的图象大致为( )A、 B、
B、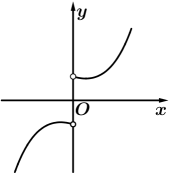 C、
C、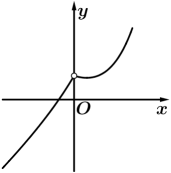 D、
D、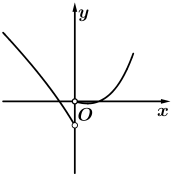 7. 已知函数 在 上为减函数,则 的取值范围是( )A、 B、 C、 D、8. 已知函数(a>0,且a≠1),若对于任意 , 恒成立,则a的取值范围是( )A、(1,2) B、(0,) C、(0,1) D、(1,+∞)
7. 已知函数 在 上为减函数,则 的取值范围是( )A、 B、 C、 D、8. 已知函数(a>0,且a≠1),若对于任意 , 恒成立,则a的取值范围是( )A、(1,2) B、(0,) C、(0,1) D、(1,+∞)二、多选题
-
9. 已知函数f(x)=xa的图象经过点( , 2),则( )A、f(x)的图象经过点(2,4) B、f(x)的图象关于原点对称 C、f(x)在(0,+∞)上单调递增 D、f(x)在(0,+∞)内的值域为(0,+∞)10. 已知函数 , 则下列说法正确的是( )A、函数在上单调递增 B、函数在上单调逆减 C、函数的最小值为0 D、函数的最小值为11. 已知x>0,y<0,且x+y=1,则( )A、 B、 C、 D、12. 若函数 在[0,2]上的最大值为2,则a的取值可以为( )A、1 B、3 C、 D、
三、填空题
-
13. 函数f(x)=a1-x+2(a>0,且a≠1)的图象所过定点的坐标为.14. 若(a>0),则m=.15. 国庆期间,高一某班31名学生去电影院观看了《长津湖》《我和我的父辈》《峰爆》这三部电影.其中有15人观看了《长津湖》,有14人观看了《我和我的父辈》,有11人观看了《峰爆》,没有人同时观看这三部电影,则仅观看了其中一部电影的共有人.16. 定义在R上的奇函数f(x)满足对任意的x1 , x2 , 当x1+x2≠0时,都有 , 则不等式f(x+1)<f(x2-1)的解集为.
四、解答题
-
17. 知集合 , .(1)、求 ;(2)、求 , .18. 已知定义在R上的函数为偶函数.(1)、求a的值;(2)、判断在上的单调性,并用定义法证明.19. 已知命题 ;命题 .(1)、若命题p为真命题,求a的取值范围;(2)、若命题p , q一真一假,求a的取值范围.20. 已知函数.(1)、若 , 求不等式的解集;(2)、若关于的方程有解,求的取值范围.