河北省邢台市临西县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2022-08-19 类型:期末考试
一、单选题
-
1. 下列式子中,不是二次根式的是( )A、 B、 C、 D、2. 以下列长度的三条线段为三边的三角形,能组成直角三角形的一组是( )A、2,5,6 B、2,3,4 C、1,1, D、1, ,3. 已知一组数据2,2,5,x,5,3有唯一的众数5,则x的值是( )A、3 B、5 C、2 D、无法确定4. 一辆汽车以60km/h的速度行驶,行驶的路程与行驶的时间t(h)之间的关系式为s=60t,其中变量是( )A、速度与路程 B、速度与时间 C、路程与时间 D、三者均为变量5. 下列计算正确的是( )A、 =2 B、 ﹣ =1 C、2+ =2 D、 =6. 已知点A的坐标为(1,-2),则点A到坐标原点的距离是( )A、 B、2 C、 D、37. 已知▱ABCD的周长为32,AB=4,则BC的长为 ( )
A、4 B、12 C、24 D、288. 某校要从甲、乙两名应聘者中招聘一名教师,该校预先对两名应聘者进行测试,每项满分100分,成绩如表所示:项目
教学设计
课堂教学
面试答辩
甲
85
90
80
乙
89
85
82
学校决定将教学设计、课堂教学、面试答辩三项得分按2:5:3的比例确定每人成绩,则将被录取的是( )
A、甲 B、乙 C、甲、乙均可 D、无法确定9. 在下列图象中,表示y是x的函数的是( )A、 B、
B、 C、
C、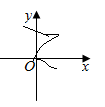 D、
D、 10. 如图,一个圆桶底面直径为8cm,高为12cm,则桶内所能容下的最长木棒的长度为( ).
10. 如图,一个圆桶底面直径为8cm,高为12cm,则桶内所能容下的最长木棒的长度为( ).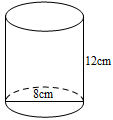 A、8cm B、10cm C、 D、11. 若+2 +=10,则x的值为( )A、4 B、±4 C、2 D、±212. 若是y关于x的正比例函数,如果点和点在该函数的图象上,那么a和b的大小关系是( )A、a<b B、a>b C、 D、13. 如图,在中,EF=2,AB=5,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,则AD的值为( )
A、8cm B、10cm C、 D、11. 若+2 +=10,则x的值为( )A、4 B、±4 C、2 D、±212. 若是y关于x的正比例函数,如果点和点在该函数的图象上,那么a和b的大小关系是( )A、a<b B、a>b C、 D、13. 如图,在中,EF=2,AB=5,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,则AD的值为( ) A、4 B、6 C、8 D、1014. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )
A、4 B、6 C、8 D、1014. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )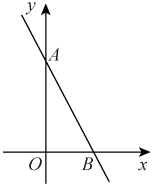 A、 B、x>3 C、 D、x<3
A、 B、x>3 C、 D、x<3二、填空题
-
15. 已知 , .(1)、 .(2)、求的值为 .16. 小红周末从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图所示的是她本次去舅舅家所用的时间与离家的距离的关系示意图.根据图中提供的信息回答下列问题.
 (1)、小红中途折回到商店所走的路程是米.(2)、小红在商店买好礼物后赶去舅舅家的速度是米/分钟.17. 如图所示的是我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形,若大正方形的边长为5,小正方形的边长为1.
(1)、小红中途折回到商店所走的路程是米.(2)、小红在商店买好礼物后赶去舅舅家的速度是米/分钟.17. 如图所示的是我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形,若大正方形的边长为5,小正方形的边长为1.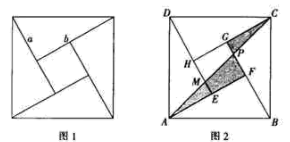 (1)、如图1,若用a,b表示直角三角形的两条直角边(a<b),则ab= .(2)、如图2,若拼成的大正方形为正方形ABCD,中间的小正方形为正方形EFGH,连接AC,交BG于点P,交DE于点M,= .
(1)、如图1,若用a,b表示直角三角形的两条直角边(a<b),则ab= .(2)、如图2,若拼成的大正方形为正方形ABCD,中间的小正方形为正方形EFGH,连接AC,交BG于点P,交DE于点M,= .三、解答题
-
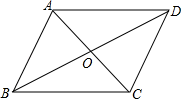
18. 计算: .19. 如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.
 20. 已知y-4与x成正比例,且当x=-1时, .(1)、求y与x的函数关系式(2)、当时,求x的值.21. 在学校组织的知识竞赛中,每班参加竞赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
20. 已知y-4与x成正比例,且当x=-1时, .(1)、求y与x的函数关系式(2)、当时,求x的值.21. 在学校组织的知识竞赛中,每班参加竞赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图: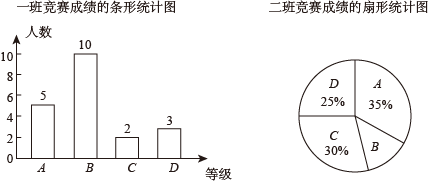
请你根据以上提供的信息解答下列问题:
(1)、求一班参赛选手的平均成绩.(2)、此次竞赛中,二班成绩在C等级以上(包含C等级)的人数是多少?22. 我们用表示不大于a的最大整数,的值称为数a的相对小数部分.如[2.13]=2,2.13的相对小数部分为2.13-[2.13]=0.13.(1)、 , 的相对小数部分= , -3.2的相对小数部分= .(2)、设的相对小数部分为m,求的值.23. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于点A,B,点在直线上. (1)、求点A,B的坐标.(2)、若C是x轴的负半轴上一点,且 , 求直线PC的表达式.(3)、在(2)的条件下,若E是直线AB上一动点,过点E作轴交直线PC于点Q,EM⊥x轴,QN⊥x轴,垂足分别为M,N,是否存在点E,使得四边形EMNQ为正方形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
(1)、求点A,B的坐标.(2)、若C是x轴的负半轴上一点,且 , 求直线PC的表达式.(3)、在(2)的条件下,若E是直线AB上一动点,过点E作轴交直线PC于点Q,EM⊥x轴,QN⊥x轴,垂足分别为M,N,是否存在点E,使得四边形EMNQ为正方形?若存在,请直接写出点E的坐标;若不存在,请说明理由.